Triangle from median
Calculate the perimeter, area, and magnitudes of the triangle ABC's remaining angles: a = 8.4; β = 105° 35 '; and median ta = 12.5.
Correct answer:
Tips for related online calculators
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- planimetrics
- perimeter
- triangle
- The Law of Cosines
- goniometry and trigonometry
- cosine
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Similarity coefficient
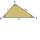The triangles ABC and A'B'C' are similar to the similarity coefficient 2. The sizes of the angles of the triangle ABC are α = 35° and β = 48°. Find the magnitudes of all angles of triangle A'B'C'. - The triangles
The triangles ABC and A'B'C 'are similar, with a similarity coefficient of 2. The angles of the triangle ABC are alpha = 35° and beta = 48°. Determine the magnitudes of all angles of triangle A'B'C '. - Median
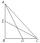In the ABC triangle is given side a=10 cm and median to side a: ta= 13 cm, and angle gamma 90°. Calculate the length of the median to side b (tb). - Calculate 4425
In the triangle ABC with the center of gravity T, b = 7cm, median to c: tc = 9cm, the ATC angle is 112 degrees. Calculate the length of the line ta.
- Perimeter 6002
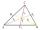In the triangle ABC, there is a side c = 5cm and medians ta = 6cm (median to side a), tb = 4.5cm (median to side b). Find the perimeter of the triangle ABT (T = center of gravity). - Angles of a triangle
In triangle ABC, the angle beta is 15° greater than the angle alpha. The remaining angle is 30° greater than the sum of the angles alpha and beta. Calculate the angles of a triangle. - Hypotenuses 83154
In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10. Calculate the side sizes of triangle ABC and the circle's radius described by this triangle.
