Thaletova věta - příklady
Thaletova věta říká, že pokud A, B, C jsou body na kružnici, kde AC je průměr kružnice, pak úhel ABC je pravý úhel. Thaletova kružnice je množina vrcholů pravých úhlů pravoúhlých trojúhelníků sestrojených nad průměrem kružnice. Thaletova věta přímo vyplývá z věty o středovém a obvodvom úhlu. Důkaz pomocí úhlů - poloměr spojující bod C dělí pravoúhlý trojúhelník na dva rovnoramenné + součet úhlů v každém trojúhelníku je 180 °.Pokyny: Vyřešte každý úkol pečlivě a ukažte své celé řešení. Pokud je to vhodné, proveďte zkoušku správnosti řešení.
Počet nalezených příkladů: 45
- Pomocí
Pomocí Euklidových vět zkonstruujte trojúhelník ABC s výškou na stranu c o velikosti v = √8 cm. Délku přepony c si správně zvolte. Napište postup konstrukce. - Úhlopříčky 80719
Sestroj obdélník ABCD pokud a = 8cm a délka úhlopříčky AC je 13cm. Změř délku stran obdélníku. - Do kruhu
Do kruhu s průměrem 20cm byl vepsán pravoúhlý trojúhelník, jehož přepona je průměrem kruhu má co největší obsah. Vypočítej obsah tohoto trojúhelníku. - Trojúhelník 73464
Daná je úsečka BC délky 6cm. Sestroj trojúhelník tak, aby úhel BAC měl velikost 50° a výška na stranu a měla 5,5 cm. Děkuji pěkně.
- Trojúhelník 67504
Sestroj trojúhelník HOP, pokud o=6 cm, h=8 cm a |PHO|=90° - Čtyřúhelník 67384
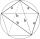Sestrojte čtyřúhelník ABCD, pokud AB=10cm, AD=6cm, DC=6,5cm a úhel BCD=90 stupňů - Sestroj 19
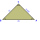Sestroj pravoúhlý trojúhelník ABC s přeponou AB: a) |AB|=72 mm, |BC|=51 mm b) |AB|=58 mm, |AC|= 42 mm - Hippokratovy měsíčky.
Vypočítejte součet obsahů tzv. Hippokratových měsíčků, které byly setrojeny nad odvěsnami pravoúhlého trojúhelníka (a=6cm, b=8cm). Návod: vypočítejte nejprve obsahy polokruhů nad všemi stranami trojúhelníka ABC. Porovnejte součet obsahů měsíčků s obsahem - Sestroj 16
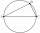Sestroj pravoúhlý trojúhelník MNO, prepona o = 5 cm, úhel MNO = 37°
- Bod A
Bod A má od kružnice o poloměru r = 4cm a středem S vzdálenost IA, kl = 10 cm. Vypočítejte: a) vzdálenost bodu A od bodu dotyku T, pokud je tečna ke kružnici vedena z bodu A b) vzdálenost dotykového bodu T od spojnice SA - MIT 1869
Znáte délku částí 9 a 16, na které přeponu pravoúhlého trojúhelníku rozdělí kolmice spuštěná z jeho protilehlého vrcholu. Úkolem je zjistit délky stran trojúhelníku a délku úsečky x. Tato úloha byla součástí přijímacích zkoušek na Massachusettský technolo - Kosodélník
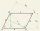Sestrojte kosodélník ABCD se stranou a=7cm, b=5cm, jehož úhlopříčka e je kolmá na stranu b. - Kosodélník a čtverec
Sestrojte čtverec, který má obsah jako kosodélník ABCD ak |AB|=5cm, |AD|=4cm a úhel |DAB|=30° - Narýsuj 7
Narýsuj pravoúhlý trojúhelník, který má stranu a = 5 cm, c = 8 cm. Pravý úhel je u vrcholu C. Jaká je velikost strany b? *
- Amfiteátr
Amfiteátr má tvar půlkruhu, diváci sedí na obvodu půlkruhu, pódium tvoří průměr půlkruhu. Který z diváků P, Q, R, S, T vidí pódium pod největším zorným úhlem? - V pravoúhlém 2
V pravoúhlém trojúhelníku ABC jsou známy tyto prvky: a = 10 cm, vc = 9,23 cm. Vypočítejte o, R (poloměr opsané kružnice), r (poloměr vepsané kružnice). - Sestrojte kosočtverec
Sestrojte kosočtverec ABCD, jestliže je dána délka úhlopříčky | AC | = 8cm, poloměr vepsané kružnice r = 1,5cm - Rovnoběžky a jedna sečna
Jsou dány dvě různé rovnoběžné přímky a, b a přímka c, která obě rovnoběžky protíná. Sestrojte kružnici, která se dotýká současně všech zadaných přímek. - Z8 – I – 1 MO 2019
Sestrojte kosočtverec ABCD tak, aby jeho úhlopříčka BD měla velikost 8 cm a vzdálenost vrcholu B od primky AD byla 5 cm. Určete všechny možnosti
Daná je kružnice k(O; 2,5cm), přímka p: /Op/=4 cm, bod T: T patří p a zároveň /OT/=4,5 cm. Máme nalézt všechny kružnice, které se budou dotýkat kružnice k a zároveň přímky p v bodě T.Máš příklad, nad kterým si přemýšlíš alespoň 10 minut? Pošli nám příklad a my Ti ho zkusíme vypočítat.
