Hippokratovy měsíčky.
Vypočítejte součet obsahů tzv. Hippokratových měsíčků, které byly setrojeny nad odvěsnami pravoúhlého trojúhelníka (a=6 cm, b=8 cm). Návod: vypočítejte nejprve obsahy polokruhů nad všemi stranami trojúhelníka ABC. Porovnejte součet obsahů měsíčků s obsahem trojúhelníka ABC.
Vaše odpověď:
Vaše odpověď:
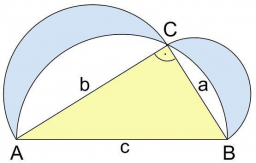
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriearitmetikaplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Trojúhelník PT
Vypočítejte obsah pravoúhlého trojúhelníku ABC s odvěsnami a=15 cm, b=1,7 dm. - Obsah pravoúhlého trojúhelníku
Obvod pravoúhlého trojúhelníku je 18 cm. Součet obsahů čtverců sestrojených nad jeho třemi stranami je 128 cm². Jaký je obsah trojúhelníku. - Součet čtverců
Součet čtverců nad stranami pravoúhlého trojúhelníku je 900 cm². Vypočítejte jaký je obsah čtverce nad přeponou tohoto trojúhelníku! - Pravoúhlý - proměna
Z pravoúhlého trojúhelníku s odvěsnami 23 cm a 23 cm jsme sestrojili čtverec se stejným obsahem jako trojúhelník. Jak dlouhá bude strana čtverce? - Rotace
Vypočítejte povrch a objem kužele, který vznikne rotací pravoúhlého trojúhelníku ABC s odvěsnami dlouhými 6 cm a 9 cm kolem kratší odvěsny. - Vypočtěte 26
Vypočtěte objem a povrch hranolu s podstavou pravoúhlého trojúhelníka s odvěsnami o délce 40 a 43 cm. Výška hranolu je 60 cm. - Tangens 2
Tangens úhlu tvořeného sousedními stranami trojúhelníka ABC (strana a=29 m, b = 40 m) je roven 1,05. Spočítejte obsah toho trojúhelníka.
