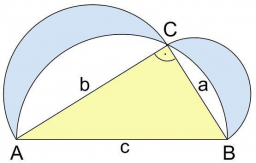
Hippokratové mesiačiky
Vypočítajte súčet obsahov tzv. Hippokratových mesiačikov, ktoré boli zostrojené nad odvesnami pravouhlého trojuholníka (a=6 cm, b=8 cm). Návod: vypočítajte najprv obsahy polkruhov nad všetkými stranami trojuholníka ABC. Porovnajte súčet obsahov nechtíkov s obsahom trojuholníka ABC.
Vaša odpoveď:
Vaša odpoveď:
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
geometriaaritmetikaplanimetriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Polovica obĺžnika
Vypočítajte obsah pravouhlého trojuholníka ABC s odvesnami a=15 cm, b=1,7 dm. - Obvod 26
Obvod pravouhlého trojuholníka je 18 cm. Súčet obsahov štvorcov zostrojených nad jeho troma stranami je 128 cm². Aký je obsah trojuholníka. - Trojuholníky - PT2
Nad odvesnami a preponou sú zostrojené štvorce. Spojením vonkajších vrcholov susedných štvorcov vzniknú tri trojuholníky. Dokáž, že ich obsahy sú rovnaké. - Súčet 14
Súčet štvorcov nad stranami pravoúhleho trojuholníka je 900 cm². Vypočítaj aký je obsah štvorca nad preponou tohto trojuholníka! - Štvorce
Na dvoma stranami trojuholníka ABC sú zostrojené štvorce. Obsah štvorca nad stranou BC je 25 cm². Veľkosť výšky vc na stranu AB je 3 cm. Pata P výšky vc delí stranu AB v pomere 2:1. Strana AC je dlhšia ako strana BC. Vypočítajte v cm dĺžku strany AB. Vypo - Pravouhlý - premena
Z pravouhlého trojuholníka s odvesnami 10 cm a 25 cm sme zostrojili štvorec s rovnakým obsahom ako trojuholník. Aká dlhá bude strana štvorca? - Trojuholník - opísaná
Vypočítajte obvod kružnice opísanej pravouhlého trojuholníka s odvesnami o delke 10 cm a 15 cm.
