Tálesova veta - príklady
Tálesova veta hovorí, že ak A, B, C sú body na kružnici, kde AC je priemer kružnice, potom uhol ABC je pravý uhol. Tálesová kružnica je množina vrcholov pravých uhlov pravouhlých trojuholníkov zostrojených nad priemerom kružnice. Tálesova veta priamo vyplýva z vety o stredovom a obvodvom uhle. Dôkaz pomocou uhlov - polomer spájajúci bod C delí pravouhlý trojuholník na dva rovnoramenné + súčet uhlov v každom trojuholníku je 180°.Pokyny: Každý problém vyriešte opatrne a krok za krokom napíšte, ako ste ho vyriešili.
Počet nájdených príkladov: 45
- Konštrukcia - EV
Pomocou Euklidových viet skonštruujte trojuholník ABC s výškou na stranu c o veľkosti v = √8 cm. Dĺžku prepony c si správne zvoľte. Napíšte postup konštrukcie. - Zostroj 21
Zostroj obdĺžnik ABCD ak a=8cm a dĺžka uhlopriečky AC je 13cm. Odmeraj dĺžku strán obdĺžnika. - Trojuholníka PT-20
Do kruhu s priemerom 20 cm bol vpísaný pravouhlý trojuholník, ktorého prepona je priemerom kruhu má čo najväčší obsah. Vypočítaj obsah tohto trojuholníka. - Strana výška a uhol
Daná je úsečka BC dĺžky 6cm. Zostroj trojuholník tak, aby uhol BAC mal veľkosť 50°a výška na stranu a mala 5,5 cm. Ďakujem pekne. - Zostroj 20
Zostroj trojuholník HOP, ak o=6 cm, h=8cm a |PHO|=90° - Zostrojte 11
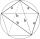Zostrojte štvoruholník ABCD, ak AB=10cm, AD=6cm, DC=6,5cm a uhol BCD=90 stupňov - Zostrojenie trojuholníka
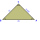Zostrojte pravouhlý trojuholník ABC s preponou AB: a) | AB | = 72 mm, | BC | = 51 mm b) | AB | = 58 mm, | AC | = 42 mm - Hippokratové mesiačiky
Vypočítajte súčet obsahov tzv. Hippokratových mesiačikov, ktoré boli zostrojené nad odvesnami pravouhlého trojuholníka (a=6cm, b=8cm). Návod: vypočítajte najprv obsahy polkruhov nad všetkými stranami trojuholníka ABC. Porovnajte súčet obsahov nechtíkov s - Prepona o
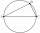Zostroj pravouhlý trojuholník MNO, prepona o = 5 cm, uhol MNO = 37° - Bod dotyku
Bod A má od kružnice s polomerom r = 4cm a stredom S vzdialenosť IA, kl = 10 cm. Vypočítajte: a) vzdialenosť bodu A od bodu dotyku T, ak je dotyčnica ku kružnici vedená z bodu A b) vzdialenosť dotykového bodu T od spojnice SA - MIT 1869
Poznáte dĺžku častí 9 a 16, na ktoré preponu pravouhlého trojuholníka rozdelí kolmica spustená z jeho protiľahlého vrcholu. Úlohou je zistiť dĺžky strán trojuholníka a dĺžku úsečky x. Táto úloha bola súčasťou prijímacích skúšok na Massachusetts Institute - Zostrojte 7
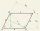Zostrojte kosodlžník ABCD so stranou a=7cm, b=5cm, ktorého uhlopriečka e je kolmá na stranu b. - Zostrojte 6
Zostrojte štvorec, ktorý má obsah ako kosodĺžnik ABCD ak/AB/=5cm, /AD/=4cm a uhol |DAB|=30° - Pravouhlý trojuholník
Narysuj pravouhlý trojuholník, ktorý má stranu a = 5 cm, c = 8 cm. Pravý uhol je pri vrchole C. Aká je veľkosť strany b? - Amfiteáter 2
Amfiteáter má tvar polkruhu, diváci sedia na obvode polkruhu, pódium tvorí priemer polkruhu. Ktorý z divákov P, Q, R, S, T vidí pódium pod najväčším zorným uhlom? - Vpísaná a opísaná
V pravouhlom trojuholníku ABC sú známe tieto prvky: a = 10 cm, vc = 9,23 cm. Vypočítajte o, R (polomer opísanej kružnice), r (polomer vpísanej kružnice). - Zostrojte 4
Zostrojte kosoštvorec ABCD, ak je daná dĺžka uhlopriečky |AC|=8cm, polomer vpísanej kružnice r=1,5cm - Rovnobežky a jedna sečnica
Sú dané dve rôzne rovnobežné priamky a, b a priamka c, ktorá obe rovnobežky pretína. Zostrojte kružnicu, ktorá sa dotýka súčasne všetkých zadaných priamok. - Z8 – I – 1 MO 2019
Zostrojte kosoštvorec ABCD tak, aby jeho uhlopriečka BD mala veľkosť 8 cm a vzdialenosť vrcholu B od priamky AD bola 5 cm. Určte všetky možnosti. Aká je dĺžka strany kosoštvorca? - Nájsť kružnice
Daná je kružnica k(O; 2,5cm), priamka p: /Op/=4 cm, bod T: T patrí p a zároveň /OT/=4,5 cm. Máme nájsť všetky kružnice, ktoré sa budú dotýkať kružnice k a zároveň priamky p v bode T.
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám príklad a my Ti ho skúsime vypočítať.
