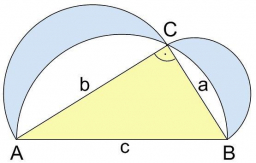
Lunes of Hippocrates
Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the areas of the lunas with the area of the triangle ABC.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- Thales' theorem
- arithmetic
- comparing
- planimetrics
- Pythagorean theorem
- right triangle
- circle
- area of a shape
- circular sector
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Infinite sum of areas
An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the - Rectangular triangles
The lengths of corresponding sides of two rectangular triangles are in the ratio 2:5. At what ratio are medians relevant to hypotenuse these right triangles? At what ratio are the areas of these triangles? A smaller rectangular triangle has legs 6 and 8 c - Constructed 8161
The perimeter of the right triangle is 18 cm. The sum of the areas of the squares constructed above its three sides is 128cm². What is the area of the triangle? - Right triangle ABC
Calculate the perimeter and area of a right triangle ABC. If you know the length of the legs, 4 cm, 5.5 cm, and 6.8 cm are the hypotenuse. - Recursion squares
In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 22 cm. Calculate: a) the sum of peri - Right triangle
Right triangle ABC with side a = 19 and the area S = 95. Calculate the length of the remaining sides. - Medians and sides
Triangle ABC in the plane Oxy; are the coordinates of the points: A = 2.7 B = -4.3 C-6-1 Try to calculate the lengths of all medians and all sides. - Right-angled 40961
A right-angled triangle ABC has sides a = 5 cm, b = 8 cm. The similar triangle A'B'C' is 2.5 times smaller. Calculate what percentage of the area of triangle ABC is the area of triangle A'B'C'. - Sum of squares
The sum of squares above the sides of the rectangular triangle is 900 cm². Calculate the area of the square over the triangle's hypotenuse. - Construct 1
Construct a triangle ABC, a = 7 cm, b = 9 cm with a right angle at C, and construct the axis of all three sides. Measure the length of side c (and write). - Triangular prism
Calculate the surface of a triangular prism 10 cm high, the base of which is a triangle with sides of 6 cm, 8 cm, and 8 cm - Equilateral 4301
Triangle ABC is equilateral with a side length of 8 cm. Points D, E, and F are the sides AB, BC, and AC midpoints. Calculate the area of triangle DEF. In what ratio is the area of triangle ABC to the area of triangle DEF? - Calculate 4424 Calculate the area of the triangle ABC if a = 10 cm, c = 8 cm, ta = 6 cm.
- Calculate 72624
The perimeter of the ABC triangle is 19.6 cm. The following applies to the lengths of its sides: a: c = 1:2, b: c = 5:6. Calculate the lengths of all sides of the triangle ABC. - Squares above sides
Two squares are constructed on two sides of the ABC triangle. The square area above the BC side is 25 cm². The height vc to the side AB is 3 cm long. The heel P of height vc divides the AB side in a 2: 1 ratio. The AC side is longer than the BC side. Calc - Squares above sides
In a right triangle, the areas of the squares above its sides are 169, 25, and 144. The length of its longer leg is: - Median in right triangle
In the rectangular triangle, ABC has known the length of the legs a = 15cm and b = 36cm. Calculate the length of the median to side c (to hypotenuse).
