PT - Pythagorean

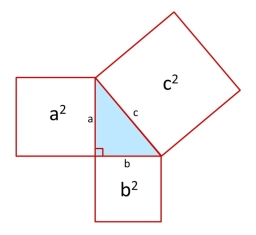
A right triangle ABC has hypotenuse c and legs a and b. Estimate the length of the missing side and compare your estimate with the calculated value.

a) a = 4 cm; b = 5 cm
b) a = 6.8 m; b = 9 m
c) a = 8.9 m; b = 1 m
d) b = 10 cm; c = 20 cm
e) b = 2.5 m; c = 400 cm

Your answer:

Help us improve! If you spot a mistake, please let let us know. Thank you!

Tips for related online calculators

You need to know the following knowledge to solve this word math problem:

algebra

rearrange variables

arithmetic

square root

planimetry

Pythagorean theorem
right triangle

Grade of the word problem

practice for 13 year olds
practice for 14 year olds

We encourage you to watch this tutorial video on this math problem: video1 video2

Related math problems and questions:

Median in right triangle
In the rectangular triangle, ABC has known the length of the legs a = 15 cm and b = 36 cm. Calculate the length of the median to side c (to hypotenuse).
RT = legs, circle
One leg of a right triangle ABC has length a= 14 cm and the radius of the circle inscribed in this triangle r= 5 cm. Calculate the length of the hypotenuse and its other leg.
Right triangle ABC
Calculate the perimeter and area of a right triangle ABC. If you know the length of the legs, 4 cm, 5.5 cm, and 6.8 cm are the hypotenuse.
Right-angled - legs
The lengths of legs are a = 7.2 cm and b = 10.4 cm in the right-angled triangle ABC. Calculate: a) lengths of the sections of the hypotenuse b) height to the hypotenuse c
Euclid2
Right triangle ABC has a right angle at C, with side a = 29 and altitude from C to the hypotenuse h = 17. Calculate the perimeter of the triangle.
Triangle height ratio
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC.
Right triangle - ratio
The lengths of the legs of the right triangle ABC are in ratio b = 2:3. The hypotenuse is 10 cm long. Calculate the lengths of the legs of that triangle.