Median in right triangle
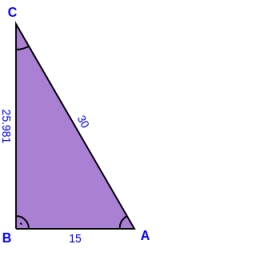
In the rectangular triangle, ABC has known the length of the legs a = 15cm and b = 36cm. Calculate the length of the median to side c (to hypotenuse).
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsGrade of the word problem
Related math problems and questions:
- Triangle KLM
In the rectangular triangle KLM, where |KL|=m is the hypotenuse (sketch it!). Find the length of the leg k and the height of triangle h if the hypotenuse's segments are known MK = 5cm and ml = 15 cm. - The right triangle
The right triangle ABC has a leg a = 36 cm and an area S = 540 cm². Calculate the length of the leg b and the median t2 to side b. - RT = legs, circle
One leg of a right triangle ABC has length a= 14 cm and the radius of the circle inscribed in this triangle r= 5 cm. Calculate the length of the hypotenuse and its other leg. - PT - Pythagorean
A right triangle ABC has hypotenuse c and legs a, and b of the following lengths. Estimate the length of its remaining side and compare your estimates with your calculations. a) a = 4 cm; b = 5 cm b) a = 6.8 m; b = 9 m c) a= 8.9 m; b = 1 m d) b= 10 cm; c - Right-angled - legs
The lengths of legs are a = 7.2 cm and b = 10.4 cm in the right-angled triangle ABC. Calculate: a) lengths of the sections of the hypotenuse b) height to the hypotenuse c - In a right-angled 15 In a right-angled triangle ABC with hypotenuse c, the length of the side b = 4.5 cm and tan α = 2/3. What is the length of the side a?
- Median
In the right triangle are sides a=96 dm b=31 dm. Calculate the length of the medians tc to the hypotenuse.
