MIT 1869
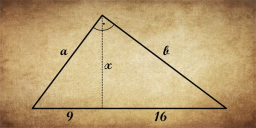
Znáte délku částí 9 a 16, na které přeponu pravoúhlého trojúhelníku rozdělí kolmice spuštěná z jeho protilehlého vrcholu. Úkolem je zjistit délky stran trojúhelníku a délku úsečky x. Tato úloha byla součástí přijímacích zkoušek na Massachusettský technologický institut MIT v roce 1869.
Vaše odpověď:
Vaše odpověď:
Zobrazuji 2 komentáře:
Žák
Jednodušší řešení téměř bez počítání. Protože všechny 3 zadané trojúhelníky jsou si podobné platí: x/9 = 16/x => x = 12. A protože každý trojúhelník, který má poměr stran 3:4:5 je pravoúhlý, musí platit: a = 3*5 = 15 a b = 4*5 = 20.
PS: Třeba tenkrát chtěli na MIT vědět, kdo jen počítá a kdo i přemýšlí.
PS: Třeba tenkrát chtěli na MIT vědět, kdo jen počítá a kdo i přemýšlí.
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometrieplanimetrieÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Obsah trojúhelníku ABC
Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3 - Trojúhelník KLB
Je dán rovnostranný trojúhelník ABC. Z bodu L který je středem strany BC tohoto trojúhelníku, je spuštěna kolmice k na stranu AB. Průsečík kolmice k a strany AB je označen jako bod K. Kolik % z obsahu trojúhelníku ABC tvoří trojúhelník KLB? - Centimetre - přepona
V pravoúhlém trojúhelníku má přepona délku 24 cm. Pata výšky na přeponu ji dělí na dvě části v poměru 2:4. Jakou velikost v cm má výška na přeponu? Vypočítejte v centimetrech obvod tohoto pravoúhlého trojúhelníku. - Euklid4
Odvěsny pravoúhlého trojúhelníku mají rozměry 19 m a 86 m. Vypočítejte délky přepony a výšky na přeponu. - Konstrukce a měření strany b
Sestrojte trojúhelník ABC, pokud znáte délky jeho stran c = 5 cm, a = 4 cm a úhel ABC má velikost 60°. Změřte délku strany b v milimetrech. Jaká je délka strany b? - Trojúhelník PT - výška
Odvěsny pravoúhlého trojúhelníku mají délky 30 cm a 40 cm. Jakou velikost má výška sestrojená na přeponu trojúhelníku? - Trojúhelník
V trojúhelníku ABC se stranou BC délky 2 cm je bod K středem strany AB. Body L a M rozdělují stranu AC na tři shodné úsečky. Trojúhelník KLM je rovnoramenný s pravým úhlem u vrcholu K. Určete délky stran AB, AC trojúhelníku ABC.
