Centimetre - přepona
V pravoúhlém trojúhelníku má přepona délku 24cm. Pata výšky na přeponu ji dělí na dvě části v poměru 2:4. Jakou velikost v cm má výška na přeponu? Vypočítejte v centimetrech obvod tohoto pravoúhlého trojúhelníku.
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikaplanimetriezákladní operace a pojmyÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Trojuholník KLM
 V pravoúhlém trojúhelníku KLM, kde je přepona m (načrtněte ho!) určete délku odvěsny k a výšky na přeponu Vm=h je-li dány části přepony mk = 5cm a ml = 15cm
V pravoúhlém trojúhelníku KLM, kde je přepona m (načrtněte ho!) určete délku odvěsny k a výšky na přeponu Vm=h je-li dány části přepony mk = 5cm a ml = 15cm - Thaletova
 Vypočítejte délku Thaletově kružnice opsané pravoúhlému trojúhelníku, jehož přepona má délku 3,4 cm.
Vypočítejte délku Thaletově kružnice opsané pravoúhlému trojúhelníku, jehož přepona má délku 3,4 cm. - Kosodélník
 Kosodélník (rovnoběžník) má delší stranu dlouhou 50 cm. Velikost jeho jedné výšky je 4krát větší než velikost jeho druhé výšky. Vypočítejte v centimetrech délku kratší strany tohoto rovnoběžníku.
Kosodélník (rovnoběžník) má delší stranu dlouhou 50 cm. Velikost jeho jedné výšky je 4krát větší než velikost jeho druhé výšky. Vypočítejte v centimetrech délku kratší strany tohoto rovnoběžníku. - Odvěsny a poměr
 Pro odvěsny pravoúhlého trojúhelníku platí a : b = 6:8. Přepona má délku 61 cm. Vypočítejte obvod a obsah tohoto trojúhelníku.
Pro odvěsny pravoúhlého trojúhelníku platí a : b = 6:8. Přepona má délku 61 cm. Vypočítejte obvod a obsah tohoto trojúhelníku. - Trojúhelník PT - výška
 Odvěsny pravoúhlého trojúhelníku mají délky 30 cm a 40 cm. Jakou velikost má výška sestrojená na přeponu trojúhelníku?
Odvěsny pravoúhlého trojúhelníku mají délky 30 cm a 40 cm. Jakou velikost má výška sestrojená na přeponu trojúhelníku? - Kolmé průměty odvěsen
 V pravoúhlém trojúhelníku mají kolmé průměty odvěsen na přeponu délku 3,1 cm a 6,3 cm. Vypočti obvod tohoto trojúhelníku. Výsledek zaokrouhli na setiny centimetru.
V pravoúhlém trojúhelníku mají kolmé průměty odvěsen na přeponu délku 3,1 cm a 6,3 cm. Vypočti obvod tohoto trojúhelníku. Výsledek zaokrouhli na setiny centimetru. - Sestrojený čtverce
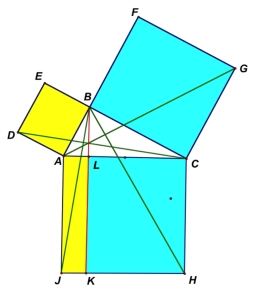
 Na dvěma stranami trojúhelníku ABC jsou sestrojeny čtverce. Obsah čtverce nad stranou BC je 25 cm². Velikost výšky vc na stranu AB je 3 cm. Pata P výšky vc dělí stranu AB v poměru 2 : 1. Strana AC je delší než strana BC. Vypočtěte v cm délku strany AB. Vy
Na dvěma stranami trojúhelníku ABC jsou sestrojeny čtverce. Obsah čtverce nad stranou BC je 25 cm². Velikost výšky vc na stranu AB je 3 cm. Pata P výšky vc dělí stranu AB v poměru 2 : 1. Strana AC je delší než strana BC. Vypočtěte v cm délku strany AB. Vy
