Euklidovy věty - příklady
Euklides byl řecký matematik a filozof. Zanechal nám dvě důležité, ale jednoduché věty, které platí v pravoúhlém trojúhelníku.První Euklidová věta (o výšce) zní: Obsah čtverce sestrojeného nad výškou pravoúhlého trojúhelníku (h) se rovná obsahu obdélníku sestrojeného z obou úseků přepony (c1 a c2):
h2=c1c2
Nebo: Výška v pravoúhlém trojúhelníku je geometrický průměr ze dvou úseků přepony.
h=c1⋅c2
Druhá Euklidová věta - o odvěsně: Obsah čtverce sestrojeného nad odvěsnou pravoúhlého trojúhelníku se rovná obsahu obdélníku sestrojeného z přepony a úseku přepony přilehlé k této odvěsně.
a2=c⋅c1
b2=c⋅c2
Nebo: Odvěsna pravoúhlého trojúhelníku je geometrický průměr přepony a přilehlého úseku přepony.
a=c⋅c1
Učí se běžně na střední škole. Použitím Euklidových vět lze snadno dokázat Pythagorova věta.
Pokyny: Každý problém vyřešte pečlivě. Ukažte celý postup.
Počet nalezených příkladů: 61
- Sestroj odmocninu
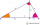 Pomocí Euklidovy věty sestrojte úsečku o délce √15.
Pomocí Euklidovy věty sestrojte úsečku o délce √15. - PT trojuhélnik
 Vypočtěte zbývající strany pravoúhlého trojúhelníku pokud známe b = 4 cm a vc = 2,4cm.
Vypočtěte zbývající strany pravoúhlého trojúhelníku pokud známe b = 4 cm a vc = 2,4cm. - Výška na stranu
 Pravoúhlý trojúhelník ABC má přeponu c dlouhou 9 cm a část přepony cb = 3 cm. Jak dlouhá je výška na stranu c?
Pravoúhlý trojúhelník ABC má přeponu c dlouhou 9 cm a část přepony cb = 3 cm. Jak dlouhá je výška na stranu c? - Rovnoramenný IV
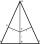 V rovnoramenném trojúhelníku ABC je |AC| = |BC| = 13. |AB| = 10. Vypočtěte poloměr vepsané (r) a opsané (R) kružnice.
V rovnoramenném trojúhelníku ABC je |AC| = |BC| = 13. |AB| = 10. Vypočtěte poloměr vepsané (r) a opsané (R) kružnice. - Kruh v kosočtverce
 Do kosočtverce je vepsán kruh. Body dotyku kruhu a kosočtverce rozdělují jeho strany na části dlouhé 12 mm a 10 mm. Vypočítejte obsah kruhu.
Do kosočtverce je vepsán kruh. Body dotyku kruhu a kosočtverce rozdělují jeho strany na části dlouhé 12 mm a 10 mm. Vypočítejte obsah kruhu. - Důkaz PV
 Lze jednoduše dokázat Pythagorovu větu pomocí Euklidových vět? Pokud ano, dokažte.
Lze jednoduše dokázat Pythagorovu větu pomocí Euklidových vět? Pokud ano, dokažte. - Euklid 5
 Vypočítejte strany pravoúhlého trojúhelníku ABC pokud: a = 7 cm, vc = 5 cm.
Vypočítejte strany pravoúhlého trojúhelníku ABC pokud: a = 7 cm, vc = 5 cm. - Strany trojúhelníku
 Vypočítejte strany trojúhelníku pokud S = 84 cm² a = x, b = x + 1, c = x + 2
Vypočítejte strany trojúhelníku pokud S = 84 cm² a = x, b = x + 1, c = x + 2 - Euklid1
 Pravoúhlý trojúhelník ABC má přeponu c = 39 cm. Jak velké úseky vytíná výška vc = 9 cm na přeponě c?
Pravoúhlý trojúhelník ABC má přeponu c = 39 cm. Jak velké úseky vytíná výška vc = 9 cm na přeponě c? - Euklid4
 Odvěsny pravoúhlého trojúhelníku mají rozměry 19 m a 86 m. Vypočítejte délky přepony a výšky na přeponu.
Odvěsny pravoúhlého trojúhelníku mají rozměry 19 m a 86 m. Vypočítejte délky přepony a výšky na přeponu. - Trojúhelník ABC
 Mějme pravoúhlý trojúhelník ABC s pravým úhlem při vrcholu C, |BC| = 20, |AB| = 35. Vypočítejte výšku vAB trojúhelníku na stranu AB.
Mějme pravoúhlý trojúhelník ABC s pravým úhlem při vrcholu C, |BC| = 20, |AB| = 35. Vypočítejte výšku vAB trojúhelníku na stranu AB. - Obsah PT
 Určitě obsah pravoúhlého trojúhelníku, jehož přepona má délku 11 a jeden její úsek (který vytíná výška) má délku 5.
Určitě obsah pravoúhlého trojúhelníku, jehož přepona má délku 11 a jeden její úsek (který vytíná výška) má délku 5. - V pravoúhlém 10
 V pravoúhlém trojúhelníku ABC jsou délky odvěsen a = 7,2 cm, b = 10,4 cm. Vypočtěte: a) délky úseků přepony b) výšku k přeponě c
V pravoúhlém trojúhelníku ABC jsou délky odvěsen a = 7,2 cm, b = 10,4 cm. Vypočtěte: a) délky úseků přepony b) výšku k přeponě c - Euklidovská vzdálenost
 Vypočítejte euklidovské vzdálenosti mezi prodejnami A, B a C, pokud: A 45 0,05 B 60 0,05 C 52 0,09 Přičemž první údaj je hmotnost pečiva v gramech a druhý je cena pečiva v €.
Vypočítejte euklidovské vzdálenosti mezi prodejnami A, B a C, pokud: A 45 0,05 B 60 0,05 C 52 0,09 Přičemž první údaj je hmotnost pečiva v gramech a druhý je cena pečiva v €. - Kolmé průměty odvěsen
 V pravoúhlém trojúhelníku mají kolmé průměty odvěsen na přeponu délku 3,1 cm a 6,3 cm. Vypočti obvod tohoto trojúhelníku. Výsledek zaokrouhli na setiny centimetru.
V pravoúhlém trojúhelníku mají kolmé průměty odvěsen na přeponu délku 3,1 cm a 6,3 cm. Vypočti obvod tohoto trojúhelníku. Výsledek zaokrouhli na setiny centimetru. - Obsah PT
 V pravoúhlém trojúhelníku mají kolmé průměty odvěsen na přeponu délku 5 cm a 8 cm. Určitě plošný obsah trojúhelníku.
V pravoúhlém trojúhelníku mají kolmé průměty odvěsen na přeponu délku 5 cm a 8 cm. Určitě plošný obsah trojúhelníku. - PT - úseky a přepona
 Vypočítej pravoúhlý trojúhelník ABC, odvěsna b=43,5 cm přepona c=72,9 cm. Vypočítej cb, a, ca, v?
Vypočítej pravoúhlý trojúhelník ABC, odvěsna b=43,5 cm přepona c=72,9 cm. Vypočítej cb, a, ca, v? - Kosočtverec a vepsaná
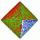 Kosočtverec má stranu a=6 cm, poloměr vepsané kružnice je r=2 cm. Vypočtěte délky obou úhlopříček.
Kosočtverec má stranu a=6 cm, poloměr vepsané kružnice je r=2 cm. Vypočtěte délky obou úhlopříček. - Euklid 9
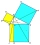 Pomocí Euklidových vět a věty Pythagorovy doplňte následující parametry popisující pravoůhlý trojůhelník ABC s pravým úhlem při vrcholu C, pokud víme b=10, cb=8
Pomocí Euklidových vět a věty Pythagorovy doplňte následující parametry popisující pravoůhlý trojůhelník ABC s pravým úhlem při vrcholu C, pokud víme b=10, cb=8 - Vypočítejte 20
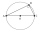 Vypočítejte strany pravoúhlého trojúhelníku, je-li zadána, že a+b=17cm, poloměr vepsané kružnice ρ=2cm.
Vypočítejte strany pravoúhlého trojúhelníku, je-li zadána, že a+b=17cm, poloměr vepsané kružnice ρ=2cm.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
