Rovnoramenný IV

V rovnoramenném trojúhelníku ABC je |AC| = |BC| = 13. |AB| = 10. Vypočtěte poloměr vepsané (r) a opsané (R) kružnice.

Správná odpověď:

r =  3,3333
R =  7,0417

Postup správného řešení:

b=13 c=10  h2 = b2 − (c/2)2 h=b2−(c/2)2​=132−(10/2)2​=12 (b−c/2)2 + r2 = (h−r)2  w=(b−c/2)2=(13−10/2)2=64  w + r2 = h2 −2hr + r2 w = h2 −2hr r=2⋅ hh2−w​=2⋅ 12122−64​=3,3333
(c/2)2 = h(2R−h)  R=2hc2/4+h2​=2⋅ 12102/4+122​=7,0417

Vyzkoušejte výpočet přes naší kalkulačku trojúhelníků.


Zkusit jiný příklad


Našel jsi chybu či nepřesnost? Klidně nám ji napiš.







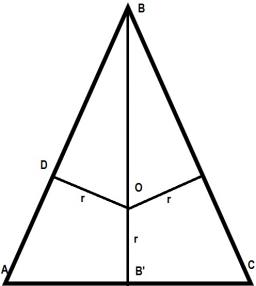
Tipy na související online kalkulačky
Naše kalkulačka pro výpočet procent Vám pomůže rychle vypočítat různé typické úlohy s procenty.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vypočet rovnoramenného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.

K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:

Úroveň náročnosti úkolu:


 
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1

Související a podobné příklady: