Rovnoramenný IV
V rovnoramennom trojuholníku ABC je |AC|=|BC| = 13. |AB| = 10. Vypočítajte polomer vpísanej (r) a opísanej (R) kružnice.
Správna odpoveď:
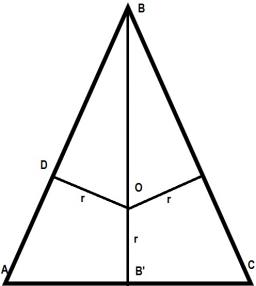
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Vypočet rovnoramenného trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vypočet rovnoramenného trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
aritmetikaplanimetriaÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- V pravouhlom 11
 V pravouhlom trojuholníku ABC vypočítajte veľkosť vnútorných uhlov, ak/AB/ = 13 cm; /BC/ = 12 cm a/AC/ = 5 cm.
V pravouhlom trojuholníku ABC vypočítajte veľkosť vnútorných uhlov, ak/AB/ = 13 cm; /BC/ = 12 cm a/AC/ = 5 cm. - Vpísaná a opísaná
 V pravouhlom trojuholníku ABC sú známe tieto prvky: a = 10 cm, vc = 9,23 cm. Vypočítajte o, R (polomer opísanej kružnice), r (polomer vpísanej kružnice).
V pravouhlom trojuholníku ABC sú známe tieto prvky: a = 10 cm, vc = 9,23 cm. Vypočítajte o, R (polomer opísanej kružnice), r (polomer vpísanej kružnice). - V trojuholníku 16
 V trojuholníku ABC poznáme a = 4 cm, b = 6 cm, γ = 60°. Vypočítajte obsah, polomer vpísanej a opísanej kružnice.
V trojuholníku ABC poznáme a = 4 cm, b = 6 cm, γ = 60°. Vypočítajte obsah, polomer vpísanej a opísanej kružnice. - Trojuholník - opísaná
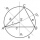 Vypočítaj dĺžky strán trojuholníka ABC, v ktorom α = 113°, β = 48° a polomer kružnice trojuholníku opísanej je r = 10 cm.
Vypočítaj dĺžky strán trojuholníka ABC, v ktorom α = 113°, β = 48° a polomer kružnice trojuholníku opísanej je r = 10 cm. - Ak trojuholník
 Ak trojuholník ABC ~ (podobný) trojuholníku XYZ, AC = 24, AB = 15, BC = 17 a XY = 9, aký je obvod trojuholníka XYZ? Zaokrúhlite všetky strany na 1 desatinné miesto.
Ak trojuholník ABC ~ (podobný) trojuholníku XYZ, AC = 24, AB = 15, BC = 17 a XY = 9, aký je obvod trojuholníka XYZ? Zaokrúhlite všetky strany na 1 desatinné miesto. - PT a kružnice
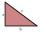 Riešte pravouhlý trojuholník, ak sú dané polomery vpísanej r=10 a opísanej kružnice R=29.
Riešte pravouhlý trojuholník, ak sú dané polomery vpísanej r=10 a opísanej kružnice R=29. - RS trojuholník
 Vypočítajte polomery kružnice vpísanej a opísanej rovnostrannému trojuholníku so stranou a=76 cm.
Vypočítajte polomery kružnice vpísanej a opísanej rovnostrannému trojuholníku so stranou a=76 cm.
