PT a kružnice
Riešte pravouhlý trojuholník, ak sú dané polomery vpísanej r=9 a opísanej kružnice R=23.
Správna odpoveď:
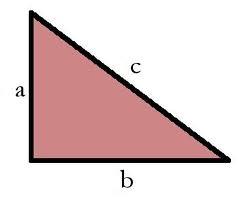
Tipy na súvisiace online kalkulačky
Hľadáte pomoc s výpočtom koreňov kvadratickej rovnice?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Trojuholníku 16223
V pravouhlom trojuholníku ABC sú známe tieto prvky: a = 10 cm, vc = 9,23 cm. Vypočítajte o, R (polomer opísanej kružnice), r (polomer vpísanej kružnice). - RS trojuholník
Vypočítajte polomery kružnice vpísanej a opísanej rovnostrannému trojuholníku so stranou a=77 cm. - Vpísana a opísana
Vypočítajte polomery kružnice vpísanej a opísanej pravidelnému päťuholníka, ktorého strana meria 3 cm. - Trojuholník
Vypočítajte obsah trojuholníka ABC, ak je dané: b = c = 17 cm, r = 19 cm (r je polomer opísanej kružnice).
- Pravidelný n-uholník
Ktorý pravidelný n-uholník má polomer opísanej kružnice r = 10 cm, a polomer vpísanej kružnice p = 9,962 cm? - Rovnoramenný IV
V rovnoramennom trojuholníku ABC je |AC|=|BC| = 13. |AB| = 10. Vypočítajte polomer vpísanej (r) a opísanej (R) kružnice. - Ťažnice v PT
V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C sú dané veľkosti ťažníc ta=5, tb=2√10. Vypočítajte veľkosti strán trojuholníka ABC a polomer kružnice opísanej tomuto trojuholníku.
