Sestrojený čtverce

Na dvěma stranami trojúhelníku ABC jsou sestrojeny čtverce. Obsah čtverce nad stranou BC je 25 cm2. Velikost výšky vc na stranu AB je 3 cm. Pata P výšky vc dělí stranu AB v poměru 2 : 1. Strana AC je delší než strana BC. Vypočtěte v cm délku strany AB.
Vypočtěte v cm2 obsah čtverce nad stranou AC.

Vaše odpověď:

cm
cm2


Našel si chybu či nepřesnost? Klidně nám ji napiš.



avatar




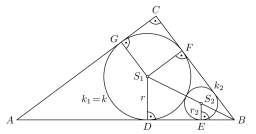
Tipy na související online kalkulačky
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.

K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:


 
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1   video2