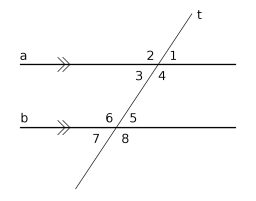
Parallels and one secant
There are two different parallel lines, a, b, and line c, that intersect the two parallel lines. Draw a circle that touches all lines at the same time.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
You need to know the following knowledge to solve this word math problem:
geometryplanimetricsUnits of physical quantitiesthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Line
Is it true that the lines that do not intersect are parallel? - Lines
How many points will intersect 27 different lines where no two are parallel? - Semicircles
In a rectangle with sides of 4cm and 8cm, there are two different semicircles, each of which has its endpoints at its adjacent vertices and touches the opposite side. Construct a square such that its two vertices lie on one semicircle, the remaining two o - Intersection of the lines
How many points do nine lines intersect in a plane, of which four are parallel, and of the other five, no two are parallel (and if we assume that only two lines pass through each intersection)?
- Intersect 5216
At how many points do ten lines intersect if no two are parallel? - Circle
The circle touches two parallel lines, p, and q, and its center lies on line a, which is the secant of lines p and q. Write the equation of the circle and determine the coordinates of the center and radius. p: x-10 = 0 q: -x-19 = 0 a: 9x-4y+5 = 0 - Diagonals 3580
Cube edge length 5cm. Draw different diagonals.
