Quatrefoil
Calculate the quatrefoil area, inscribed in a square with a side of 6 cm.
Your answer:
Your answer:
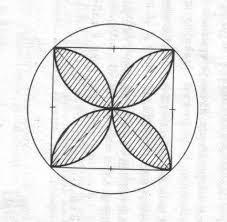
You need to know the following knowledge to solve this word math problem:
planimetryGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Quatrefoil circle radius
Gothic quatrefoil is an ornament in which four identical touching smaller circles are inscribed in a larger circle, as you can see in the picture. The radius of the great circle is one meter. Calculate the radius of the smaller circle in meters. - 6 regular polygon
A regular six-sided polygon has a side 5 cm long. Calculate its area. Compare how many more cm² (square centimeters) has a circle inscribed the 6-gon. - Pentagon
Calculate the length of a regular pentagon's side, circumference, and area, inscribed in a circle with a radius r = 6 cm. - Square circle difference
A circle is inscribed in a square with a side of 12 cm so that it touches all its sides. Calculate the difference between the area of the square and the circle. - Triangle circle calculation
The following elements are known in the right triangle ABC: a = 10 cm, height to side c h = 9.23 cm. Calculate o, R (radius of the inscribed circle), r (radius of the inscribed circle). - Rhombus and inscribed circle
It is given a rhombus with side a = 6 cm and the inscribed circle r = 2 cm radius. Calculate the length of its two diagonals. - Square circles
Calculate the length of the described and inscribed circle to the square ABCD with a side of 5 cm.
