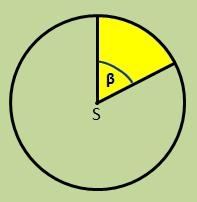
Three segments
The circle is divided into three segments. Segment A occupies 1/4 of the area. Segment B occupies 1/3 of the area. What part is occupied by section C? In what proportion are areas A: B: C?
Correct answer:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Check out our ratio calculator.
Check out our ratio calculator.
You need to know the following knowledge to solve this word math problem:
planimetricsbasic operations and conceptsnumbersUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Chord 24
A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments? - Two-fifths 5337
The triangle is divided into three parts. The part at the vertex C occupies a third of the area of the triangle, the part at the vertex B is two-fifths of the area of the triangle, and the remaining part at the vertex A has an area of 4 m². Calculate the - MO - triangles
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a - Quadrilateral 82616
Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the area of quadrilateral AFHD. - Ace
The length of segment AB is 24 cm, and the points M and N are divided into thirds. Calculate the circumference and area of this shape. - Described circle to rectangle
The rectangle with 6 cm and 4 cm sides was a circumscribed circle. What part of the circle area determined by the circumscribed circle occupies a rectangle? Express in perctentages(%). - On the circular 3
On the circular cap of a salt shaker with a diameter of 4.5 cm there are two types of holes. On the left is a semicircular hole with a diameter of 2.4 cm, on the right are five small circular holes with a diameter of 3 millimeters. Determine the ratio of
