Chord - TS v2
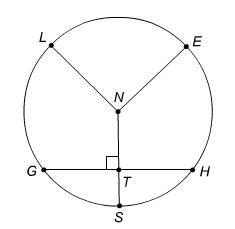
The radius of circle k measures 72 cm. Chord GH = 11 cm. What is TS?
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Chord - TS
The radius of circle k measures 68 cm. Arc GH = 47 cm. What is TS? - The formula
The formula for the area of a circle is (Pi x r x r), where r = measure of the radius and Pi = 3.14. What is the area of a circle whose radius measures 1 cm? - Concentric circles and chord
In a circle with a diameter d = 10 cm, a chord with a length of 6 cm is constructed. What radius has the concentric circle while touching this chord? - Chord
In a circle with a radius r=60 cm is the chord, 4× longer than its distance from the center. What is the length of the chord?
- Calculate 79144
The circle's radius is r=8.9 cm, and the chord AB of this circle has a length of 16 cm. Calculate the distance of chord AB from the center of the circle. - Calculate 58953
Calculate the area of a circular line if the radius r = 80 cm and the central angle is α = 110 °. - Circle chord
Calculate the length of the chord of the circle with radius r = 10 cm, the length of which is equal to the distance from the circle's center.
