Right 24
The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse, dividing it into two unequal segments. One segment is 5 cm long. What is the area of the triangle? Thank you.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsGrade of the word problem
Related math problems and questions:
- Right isosceles triangle
 The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse, dividing it into two equal segments. One segment is 5 cm long. What is the area of the triangle?
The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse, dividing it into two equal segments. One segment is 5 cm long. What is the area of the triangle? - An isosceles triangle
 An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in
An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in - Segments on the hypotenuse
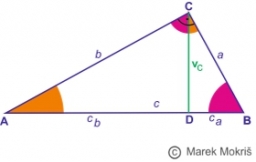
 A right triangle ABC has a hypotenuse of c=26cm. How many segments does the height vc=12 cm cut out on the hypotenuse c? What are the lengths of the sides a and b? What are the angles at the vertices A and B?
A right triangle ABC has a hypotenuse of c=26cm. How many segments does the height vc=12 cm cut out on the hypotenuse c? What are the lengths of the sides a and b? What are the angles at the vertices A and B? - Triangle KLM
 In the rectangular triangle KLM, where |KL|=m is the hypotenuse (sketch it!). Find the length of the leg k and the height of triangle h if the hypotenuse's segments are known MK = 5cm and ml = 15 cm.
In the rectangular triangle KLM, where |KL|=m is the hypotenuse (sketch it!). Find the length of the leg k and the height of triangle h if the hypotenuse's segments are known MK = 5cm and ml = 15 cm. - Hypotenuse 3554
 Calculate the hypotenuse length if you know the area of an isosceles right triangle that is 24.5 cm square.
Calculate the hypotenuse length if you know the area of an isosceles right triangle that is 24.5 cm square. - Area of RT
 Calculate the right triangle area in which the hypotenuse has length 14 and one hypotenuse segment has length 5.
Calculate the right triangle area in which the hypotenuse has length 14 and one hypotenuse segment has length 5. - Trapezoid 83
 Trapezoid ABCD is composed of five triangles. Points E, and G divide segment AB in the ratio 2:4:3 (in this order) into three segments. Point F is the midpoint of segment AD. Triangle AEF is isosceles and right-angled. Triangles GBC and CDG are right-angl
Trapezoid ABCD is composed of five triangles. Points E, and G divide segment AB in the ratio 2:4:3 (in this order) into three segments. Point F is the midpoint of segment AD. Triangle AEF is isosceles and right-angled. Triangles GBC and CDG are right-angl
