The right triangle altitude theorem - practice problems - last page
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 71
- Circles
In the circle with a radius, 7.5 cm is constructed of two parallel chords whose lengths are 9 cm and 12 cm. Calculate the distance of these chords (if there are two possible solutions, write both). - Triangle ABC
There is the triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC tr - Construction - Euclid
Using Euclid's theorems, construct a triangle ABC with height on side c and size v = √8 cm. Choose the length of the hypotenuse c correctly. Write the construction procedure. - Square equal rhombus
Construct a square that has the same area as a rhombus ABCD if |AB| = 5cm, |AD| = 4cm, and angle |DAB| = 30°. - Triangle circle calculation
The following elements are known in the right triangle ABC: a = 10 cm, height to side c h = 9.23 cm. Calculate o, R (radius of the inscribed circle), r (radius of the inscribed circle). - Hypotenuse - RT
A triangle has a hypotenuse of 55 and an altitude to the hypotenuse of 33. What is the area of the triangle? - Touch circle
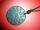
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - The bridge
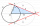
Across the circle, the lake passes through its center bridge over the lake. At three different locations on the lakeshore are three fishermen, A, B, and C. Which of the fishermen sees the bridge from the largest angle? - Euclid line construction
Using Euclid's theorem, construct a line of length √15. - Same area
There is a given triangle. Construct a square of the same area. - Conical area
A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
