Conical area
A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation.
Your answer:
Your answer:
Tips for related online calculators
Looking for a statistical calculator?
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
statisticssolid geometryplanimetryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Right angled triangle 3
Side b = 1.5, hypotenuse angle A = 70 degrees, Angle B = 20 degrees. Find the length of its unknown sides. - Prism
A right-angled prism, whose base is a right triangle with leg a = 3 cm and hypotenuse c = 6 cm, has the same volume as a cube with an edge length of 1 dm. a) Find the height of the prism b) Calculate the surface of the prism c) What percentage of the cube - Triangle rotation volume
The rotating body was created by rotating an equilateral triangle with a side length of a=2 cm around one of its sides. Calculate the volume of this rotating body. - Triangle hypotenuse circle
In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10. Calculate the side sizes of triangle ABC and the circle's radius described by this triangle. - Triangle height ratio
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC. - In a right-angled 17
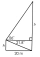In right triangle DEF with hypotenuse f = 12 cm, the interior angle at vertex D is 60°. What is the length of side e? - Propeller
The aircraft propeller rotates at an angular speed of 200 rad/s. A) What is the speed at the tip of the propeller if its distance from the axis of rotation is 1.5 m? B) What path does the aircraft travel during one propeller revolution at a speed of 540 k
