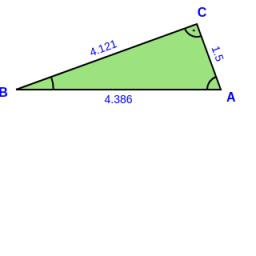
Right angled triangle 3
Side b = 1.5, hypotenuse angle A = 70 degrees, Angle B = 20 degrees. Find the length of its unknown sides.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Hypotenuse and legs
A right triangle with hypotenuse c=25 dm is given. Calculate the length of the unknown side, given: side a=15 dm. Find the area of this triangle. Sketch the triangle and describe all its vertices and sides correctly. - Right triangle
A right triangle ABC is given, and c is a hypotenuse. Find the length of the sides a, b, the angle beta if c = 5 and angle alfa = A = 35 degrees. - KLM triangle
Find the length of the sides of the triangle KLM if m = 5cm height to m = 4.5 cm and size MKL angle is 70 degrees. - Quadrilateral - irregular
Find the length of the side d = |AD| in quadrilateral ABCD: a= 35m, b= 120m, c=85m, angle ABC = 105 degrees, angle BCD= 72 degrees
- Right angle
If b=10, c=6, and c are two sides of a triangle ABC, a right angle is at the vertex A, find the value on each unknown side. - Conical area
A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation. - Millimeters 4811
Construct a triangle ABC if you know the lengths of its sides c = 5 cm, a = 4 cm and angle ABC is 60°. Measure the length of side b in millimeters. Side length b is: a, 75 mm < b < 81 mm b, 53 mm < b < 59 mm c, 43 mm < b < 49 mm d, 13 mm
