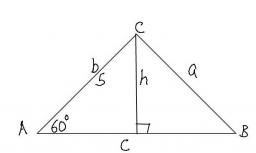
Triangle and its heights
Calculate the length of the sides of the triangle ABC if va=5 cm, vb=7 cm and side b are 5 cm shorter than side a.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Euclid 5
Calculate the length of remain sides of a right triangle ABC if a = 7 cm and height vc = 5 cm. - The triangles
Two similar triangles, KLM and ABC, are given. Calculate the lengths of the remaining sides of the triangle KLM. If the lengths of the sides are a = 7 b = 5.6 c = 4.9 k = 5 - Perimeter 16663
The sizes of the sides of a triangle are three natural numbers. The two shorter sides have lengths a = 7 cm and b = 9 cm. What size will the third side be if we want the triangle to have the largest possible perimeter? - Perimeter 5361
The sides of the triangle are a = 5.5 cm b = 3.7 cm c =? The perimeter of the triangle is 11.6 cm Calculate the length of the side c. - Triangle ABC
In an ABC triangle, side b measure 10 cm less than side a, and side b is half of side c. Calculate the length of the sides of the circumference of the triangle as 42 cm. - Right-angled 81019
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC. - Right triangle
Right triangle ABC with side a = 19 and the area S = 95. Calculate the length of the remaining sides. - Pentagonal pyramid
Calculate the volume of a regular 5-side (pentaprism) pyramid ABCDEV; if |AB| = 7.7 cm and a plane ABV, ABC has angle 37 degrees. - Three sides
Side b is 2 cm longer than side c, side a is 9 cm shorter than side b. The triangle circumference is 40 cm. Find the length of sides a, b, and c. - Construct 1
Construct a triangle ABC, a = 7 cm, b = 9 cm with a right angle at C, and construct the axis of all three sides. Measure the length of side c (and write). - Triangle ABC
Calculate the sides of triangle ABC with area 1404 cm², and if a: b: c = 12:7:18 - Rectangle vs square
One side of the rectangle is 1 cm shorter than the side of the square. The second side is 3 cm longer than the side of the square. The square and rectangle have the same area. Calculate the length of the sides of a square and a rectangle. - Squares above sides
Two squares are constructed on two sides of the ABC triangle. The square area above the BC side is 25 cm². The height vc to the side AB is 3 cm long. The heel P of height vc divides the AB side in a 2: 1 ratio. The AC side is longer than the BC side. Calc - Determine 79364
Given a general triangle ABC. Its perimeter is 30 cm, with side a=2 cm longer than side b and 5 cm shorter than side c. Determine the area of the triangle. - Similar triangles
Triangle A'B'C 'is similar to triangle ABC, whose sides are 5 cm, 8 cm, and 7 cm long. What is the length of the sides of the triangle A'B'C' if its circumference is 80 cm? - Similar triangles
The triangles ABC and XYZ are similar. Find the missing lengths of the sides of the triangles. a) a = 5 cm b = 8 cm x = 7.5 cm z = 9 cm b) a = 9 cm c = 12 cm y = 10 cm z = 8 cm c) b = 4 cm c = 8 cm x = 4.5 cm z = 6 cm - Equilateral 4301
Triangle ABC is equilateral with a side length of 8 cm. Points D, E, and F are the sides AB, BC, and AC midpoints. Calculate the area of triangle DEF. In what ratio is the area of triangle ABC to the area of triangle DEF?
