The triangles
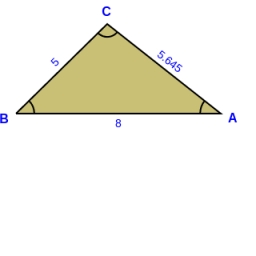
Two similar triangles, KLM and ABC, are given. Calculate the lengths of the remaining sides of the triangle KLM. If the lengths of the sides are a = 7 b = 5.6 c = 4.9 k = 5
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Circumference 42471
The lengths of the sides of the triangle ABC are in the ratio 4:2:5. Calculate the size of the longest side of a similar KLM triangle, whose circumference is 66 cm. - Similar triangles
The triangles ABC and XYZ are similar. Find the missing lengths of the sides of the triangles. a) a = 5 cm b = 8 cm x = 7.5 cm z = 9 cm b) a = 9 cm c = 12 cm y = 10 cm z = 8 cm c) b = 4 cm c = 8 cm x = 4.5 cm z = 6 cm - Triangles 2737
The triangles ABC and XYZ are similar. Find the missing lengths of the sides of the triangles. a = 5cm, b = 8cm x = 7.5cm z = 9cm - Similar triangles
In the triangle DEF is DE = 21cm, EF = 14.7cm, DF = 28cm. The triangle D'E'F' is similar to the triangle DEF. Calculate the lengths of the sides of the triangle D'E'F' if the similarity coefficient is one-seventh. - Similarity of two triangles The KLM triangle has a side length of k = 6.3cm, l = 8.1cm, m = 11.1cm. The triangle XYZ has a side length of x = 8.4cm, y = 10.8cm, z = 14.8cm. Are triangle KLM and XYZ similar? (write 0. If not, if yes, find and write the coefficient of a similarity)
- Similar triangles
Triangle A'B'C 'is similar to triangle ABC, whose sides are 5 cm, 8 cm, and 7 cm long. What is the length of the sides of the triangle A'B'C' if its circumference is 80 cm? - Following 6660
KLM triangle on sides k = 5.4 cm. L = 6 cm, m = 6.6 cm. Construct a triangle K 'L'M 'for which the following holds: ∆KLM ~ ∆K 'L'M' and m '= 9.9cm - Area and two angles
Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°. - Medians and sides
Triangle ABC in the plane Oxy; are the coordinates of the points: A = 2.7 B = -4.3 C-6-1 Try to calculate the lengths of all medians and all sides. - Similarity coefficient
In the triangle TMA, the length of the sides is t = 5cm, m = 3.5cm, and a = 6.2cm. Another similar triangle has side lengths of 6.65 cm, 11.78 cm, and 9.5 cm. Determine the similarity coefficient of these triangles and assign similar sides to each other. - Right-angled 40961
A right-angled triangle ABC has sides a = 5 cm, b = 8 cm. The similar triangle A'B'C' is 2.5 times smaller. Calculate what percentage of the area of triangle ABC is the area of triangle A'B'C'. - Right-angled 27683 Right-angled triangle XYZ is similar to triangle ABC, which has a right angle at the vertex X. The following applies a = 9 cm, x=4 cm, x =v-4 (v = height of triangle ABC). Calculate the missing side lengths of both triangles.
- Similarity
ABC is a triangle wherein a = 4 cm, b = 6 cm, c = 8 cm. Is it similar to the triangle DEF: d = 3 cm, e = 4.5 cm, f = 6 cm? If so, determine the ratio of similarity. - Sides of the triangle The sides of the triangle ABC have a length of 4 cm, 5 cm, and 7 cm. Construct triangle A'B'C', similar to triangle ABC, which has a circumference of 12 cm.
- Angles and sides of the triangle
Triangle ABC has a circumference of 26 cm. Lengths of the sides are as follows: a = 11.2 cm; b = 6.5 cm. Arrange the interior angles in order of their size. ... - Right-angled 80745
The area of a right-angled triangle KLM with a right angle at the vertex L is 60 mm square, and its hypotenuse k is 10 mm long. Triangles KLM and RST are similar. The similarity ratio is k=2.5. Calculate the area of triangle RST. - Circumference 64104
The ABC triangle has a circumference of 11 cm. Triangle A'B'C ', similar to triangle ABC, has side lengths of 6 cm, 120 mm, and 1.5 dm larger than triangle ABC. Calculate the area of the triangle A'B'C '.
