Parabola - practice problems
Direction: Solve each problem carefully and show your solution in each item.Number of problems found: 22
- What is 25
What is the trunk of 8 and 10? - Suppose 10 Suppose 4+7i is a solution of 5z²+Az+B=0, where A, B∈R. Find A and B.
- Parabola with abs
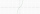A). Sketch the graph of the function f(x)=x * absolute(x) = x * |x| b). For what values of x is f(x) differentiable c). Find F(x) - Parabola 3
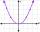Find the equation of a parabola with its focus at (0,2) and its vertex at the origin. f: y=x²+bx+c - Trapezoid and bases
Find the area of the trapezoid whose bases differ by three and whose height is three less than twice the upper base. - EQ2 - symetric results Given the function y = x² - 4x + 3. Determine all real numbers z such that g(x) = g(-2).
- Arithmetic mean - parabola
Find the value of k so that k² + 2k – 3 is the arithmetic mean between k² + 4k + 5 and k² – 6k + 10. - The sequence Find the nth term of the progression 2,6,12,20...
- Determine 83021
Determine the kinetic energy of a car with a mass of 800 kg if it travels at a speed: a) 10 m/s b) 20 m/s - Accelerated motion
The position of a mass point that moves along the x-axis is given by the relation x=10t²-5t. Express its velocity and acceleration. - A missile
A missile is fired with a speed of 100 fps in a direction 30° above the horizontal. Determine the maximum height to which it rises. Fps foot per second. - Ball
The soldier fired the Ball at an angle of 57° at an initial velocity of 186 m/s. Determine the length of the litter. (g = 9.81 m/s²). - An archer
An archer stands 60 meters (m) from a target. She launches an arrow that lands 3 centimeters (cm) from the bull's eye. The archer changes her position to 40 m from the target, and her next arrow lands 2 cm from the bull's eye. She changes her position to - Ballistic curve
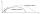The soldier fired the ballistic grenade at a 45° angle. The first half ascended, and the second fell. How far and height did it reach if his average speed was 1200 km/h, and what 12 seconds were taken from the shot to impact? - Parabolic 79764
In a tennis match, Adrien is 5 m from the net when he hits a ball 80 cm off the ground. The maximum height of its parabolic path passing through the net was 1.5 m. If the length of the court is 23.77 m, will the ball land inside the court? - Determine 82478
Determine the equation of the parabola that has the point F = [3,2] as its focus and the line x+y+1=0 as its shift line. - Determine 83003 Determine the value of the number a so that the graphs of the functions f: y = x² and g: y = 2x + a have exactly one point in common.
- Intersections 62784
A quadratic function is given: y = -x² + 2x + 3 a) determine the intersections with the x, y-axis and peak V b) draw a graph and describe c) for which x applies f (x) = 3 - Parabola
Find the equation of a parabola that contains the points at A[10; -5], B[18; -7], C[20; 0]. (use y = ax²+bx+c) - Equation 80525 Write the equation of the parabola that passes through the points: A[1,1] B[3,-1] C[1,2]
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
