Parabola 3
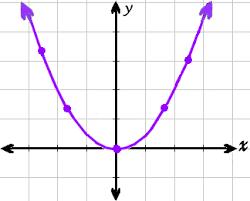
Find the equation of a parabola with its focus at (0,2) and its vertex at the origin.
f:y=x2+bx+c
f:y=x2+bx+c
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Determine 82478
Determine the equation of the parabola that has the point F = [3,2] as its focus and the line x+y+1=0 as its shift line. - Parabola
Find the equation of a parabola that contains the points at A[10; -5], B[18; -7], C[20; 0]. (use y = ax²+bx+c) - Suppose 10
Suppose 4+7i is a solution of 5z²+Az+B=0, where A, B∈R. Find A and B. - Coordinate 82855
What is the ratio of the distance of the nearest and farthest point of the circle described by the equation x2+y2-16x-12y+75=0 from the origin of the coordinate system?
- Distance
What is the distance between the origin and the point (-11; 13)? - X-coordinate 81737
In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right. - Determine 83003 Determine the value of the number a so that the graphs of the functions f: y = x² and g: y = 2x + a have exactly one point in common.
