Triangle point coordinates
In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right.
Final Answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our right triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryalgebraplanimetricsGrade of the word problem
Related math problems and questions:
- Unit circle
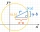In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin with coordinates (0, 0), and point B has coordinates (1, 0). The size of angle BOA is 151°. Determine the x-coordinate of point A. - In plane 2
Triangle ABC lies in the plane with a right angle at vertex C, where A(1, 2), B(5, 2), C(x, x+1), and x > −1. a) Determine the value of x. b) Determine the coordinates of point M, the midpoint of segment AB. c) Prove that vectors AB and CM are perpendi - Vertex of the rectangle
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Point construction
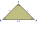Given an isosceles right triangle ABS with base AB. On a circle centered at point S and passing through points A and B, point C lies such that triangle ABC is isosceles. Determine how many points C satisfy the given conditions and construct all such point - Isosceles triangle
In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C. - Quadrilateral angle circle
The points ABC lie on the circle k(S, r) such that the angle at B is obtuse. How large must the angle at vertex B of quadrilateral SCBA be so that this angle is three times greater than the interior angle ASC of the same quadrilateral? - Chord BC
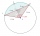A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates [- 14; 0]?
