V trojuholníku 15
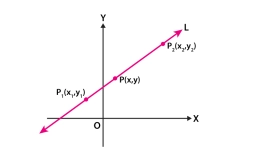
V trojuholníku ABC určte súradnice bodu B, ak viete, že body A, B ležia na priamke 3x-y-5=0, body A, C ležia na priamke 2x+3y+4=0, bod C leží na súradnicovej osi x a uhol pri vrchole C je pravý.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
geometriaalgebraplanimetriaÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Jednotková kružnica
V karteziánskej súradnicovej sústave je daná jednotková kružnica, na ktorej ležia body A a B. Bod O je počiatok a má súradnice (0,0) a bod B súradnice (1,0). Veľkosť uhla BOA je 151°. Určte x-ovú súradnicu bodu A. - Súradnice vrcholov
Určte súradnice vrcholov a obsah rovnobeznika, ktoreho dve strany ležia na priamkach 8x+3y+1=0, 2x+y-1=0 a uhlopriečka na priamke 3x+ 2y+3=0 - Trojuholníku - pravý uhol
V trojuholníku ABC zvierajú osi uhlov alpha a beta uhol φ = R + γ/2. R je pravý uhol 90°. Overte. - Mravec
Mravec lezie po súradnicovej sustave vždy rovnobežne so súradnicovými osami . Včera začal svoju puť v bode so súradnicami 0. Prešiel 20 štvorčekov po osi x urobil vlavo vbok a prešiel opať 20 štvorčekov . znovu urobil vlavo vbok a prešiel 18 štvorčekov. z - Súradnice - obdĺžnik
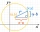Určite súradnice vrcholu obdĺžnika vpísaného do kružnice x²+y² -2x-4y-20=0, ak viete, že jedna jeho strana leží na priamke p: x+2y=0 - Body ABC
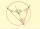Body ABC ležia na kružnici k(S, r) tak, že uhol pri B je tupý. Aký veľký musí byť uhol pri vrchole B štvoruholníka SCBA, aby bol tento uhol trikrát väčší ako vnútorný uhol ASC toho istého štvoruholníka? - Kolineárne body
Ukážte, že body A (-1,3), B (3,2), C (11,0) sú kolineárne (ležia na jednej priamke).
