Distance
What is the distance between the origin and the point (-11; 13)?
Final Answer:
Showing 1 comment:
Dr Math
The origin has coordinates (0,0). Then, use the distance formula to find the distance between the origin and the given point (x,y). The distance formula is the Pythagorean theorem applied to this problem. The resulting distance is the square root of x2 + y2.
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
geometryarithmeticplanimetricsGrade of the word problem
Related math problems and questions:
- Coordinate 82855
What is the ratio of the distance of the nearest and farthest point of the circle described by the equation x2+y2-16x-12y+75=0 from the origin of the coordinate system? - Submarine and plane
A submarine is floating 900 m below the sea level. And at the opposite point, right above the submarine, an aeroplane is flying at the height of 4800 m above the sea level. What is the vertical distance between the two? - Athletic race
Before a race, you start 4 5/8 feet behind your friend. You are 3 2/3 feet ahead of your friend at the halfway point. What is the change in distance between you and your friend from the beginning of the race? - Unit circle
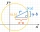In the Cartesian coordinate system, a unit circle is given on which points A and B lie. Point O is the origin and has coordinates (0,0) and point B has coordinates (1,0). The size of angle BOA is 151°. Determine the x-coordinate of point A. - Dinesh 2
Dinesh left town L for town M at a constant speed and took 10 hours to complete the journey. At the same time, Saanvi left town M for town L, traveled at a constant speed, and took 6 hours to complete the journey. They both passed each other at a point 72 - Equation of circle 2
Find the equation of a circle that touches the axis of y at a distance of 4 from the origin and cuts off an intercept of length 6 on the axis x. - Quadrilateral 78874
Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime
