An archer
An archer stands 60 meters (m) from a target. She launches an arrow that lands 3 centimeters (cm) from the bull's eye. The archer changes her position to 40 m from the target, and her next arrow lands 2 cm from the bull's eye. She changes her position to 20 m, and her next arrow lands 1 cm from the bull's eye.
Which points describe the situation when the archer stands at 40 m?
Let the x-coordinate be the archer's distance from the target in meters, and let the y-coordinate be the arrow's distance from the bull's eye in centimeters.
Which points describe the situation when the archer stands at 40 m?
Let the x-coordinate be the archer's distance from the target in meters, and let the y-coordinate be the arrow's distance from the bull's eye in centimeters.
Final Answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
Do you want to convert length units?
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsbasic operations and conceptsUnits of physical quantitiesthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Ruler
Peter is looking at John over a ruler that keeps at an arm's distance of 60 cm from the eye, and on the ruler, John measured the height of 15 mm. John is 2 meters high. How far from Peter stands John? - Shooters
In the army, regiments are piati shooters. The first shooter target hit with a probability of 42%, next with 40%, 21%, 58%, 67%. Calculate the probability of target hit when shooting all at once. - A radio antenna
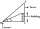Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - Clocks
What distance will describe the tip of a minute hand 6 cm long for 20 minutes when we know the starting position with finally enclosed hands at each other at 120°? - Angle of elevation
The angle of elevation of the top of an unfinished pillar at a point 150 m from its base is 30°. If the angle of elevation at the same point is to be 45°, then the pillar has to be raised to a height of how many meters? - Shooter
The shooter fired at a target from a distance 49 m. The individual concentric circle of targets has radius increments of 1 cm (25 points) by 1 point. The shot was shifted by 16' (angle degree minutes). How many points should he win his shot? - Increased 81490
Suzan managed to get 40 points out of a possible 60 from the last paper. Her average number of points from the tests increased from 27 to 28 points. How many points should she have written if she wanted her overall average to rise to 29 points?
