Triangle inequality - practice problems
In any triangle, the sum of the lengths of any two sides is greater than the length of the remaining third one.a+b > c
The triangle inequality is three inequalities that are true simultaneously. The inequalities result directly from the triangle's construction. If one side were longer than two in total, the vertex against the longest side could not be constructed (or drawn), and the triangle as a shape in the plane would not exist.
Directions: Solve each problem carefully. Show all your work.
Number of problems found: 41
- Existence of a triangle
Can the sides of a triangle have lengths 4, 18, and 20? - Triangle - same sides
Can the sides of a triangle have lengths of 11, 11, and 14? If so, what kind of triangle is it? - RST triangle
Find out if it is possible to construct the given triangle and according to which theorem: RS = 2.5 cm ST = 7 cm TR = 4.5 cm - Triangles - segments
How many triangles can be formed with segments measuring one and 2/3 mm one 3/4 mm and 2 1/2 mm - Diagonal
Can it be a diagonal diamond twice longer than its side? - 3-bracket 2
Maybe the smallest angle in the triangle is greater than 70°? - Possible lengths
Find the possible lengths for the third side of a triangle with sides 20 and 18. - Triangles - count
Find out how many triangles you create from lines 7 dm, 5 dm, 10 dm, 12 dm, and 15 dm long. - Triangle
By calculation, determine if it is possible to construct a triangle with sides 10 21 19. - QuizQ
An isosceles triangle has two sides of length 38 m and 15 m. How long is a third side? - Triangle
For how many integer values of x can 16, 10, and x be the lengths of the sides of a triangle? - Inequality triangle
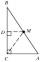The heel of height from the vertex C in the triangle ABC divides the side AB in the ratio 1:2. Prove that in the usual notation of the lengths of the sides of the triangle ABC, the inequality 3 | a-b | < c. - Triangle
Prove whether you can construct a triangle ABC if a=8 cm, b=6 cm, c=10 cm. - The perimeter
The triangle has one side 5 cm long and another 11 cm long. What can be the smallest, and what is the largest perimeter? - In an
In an ABCD square, n interior points are chosen on each side. Find the number of all triangles whose vertices X, Y, and Z lie at these points and on different sides of the square. - 3-bracket 3
Two angles in a triangle are 90° and 45°. Has the triangle at least two equal sides? - Triangle sides - natural
In triangle ABC, side a = 30 cm b = 7 cm. The length of the third side in cm is a natural number. What is the least and what is the greatest length that side c can have? - The triangle - sides The two sides of the triangle have side lengths a = 6cm and b = 13cm. Then the following applies to the length of the third side c: (A) 7
- Perimeter of a triangle If the perimeter of a triangle is 6 2/3 cm and the lengths of two sides are 2 1/2 cm and 3 1/3 cm, find the length of the third side.
- Triangle segment construction
The sum of the lengths of the three segments is 140mm. Name at least 2 triplets of segment lengths from which we can construct a triangle. Construct triangles
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
