Kvadratická rovnica kalkulačka
Kvadratická rovnica má základný tvar: ax2+bx+c=0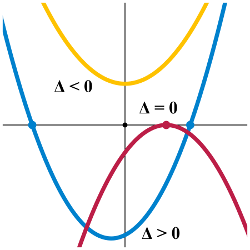
Výpočet:
Textové riešenie:
-2.2h2-h+230=0 ... kvadratická rovnicaDiskriminant:
D = b2 - 4ac = 2025
D > 0 ... Rovnica má dva rôzne reálne korene
h1 = 10
h2 = -10.4545455
P = {10; -10.4545455}
