Math practice for 13 year olds - page 23 of 422
Number of problems found: 8422
- The ratio 16
 Express the following ratio in simplest form: 90:100
Express the following ratio in simplest form: 90:100 - A miner
 A miner is working at an elevation of -64 7/9 and then ascends 22 1/3. What is the miner's new location?
A miner is working at an elevation of -64 7/9 and then ascends 22 1/3. What is the miner's new location? - Evaluate 40
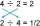 Evaluate a+bc-d if a=78, b=-716, c=0.8, and d=14 . Write your answer as a fraction in simplest form.
Evaluate a+bc-d if a=78, b=-716, c=0.8, and d=14 . Write your answer as a fraction in simplest form. - Ramit
 Ramit bought 10 pens,8 pencils, and 4 books; pens were Rs.5 1/2 each, pencils were Rs.2 1/2 each and books were Rs. 11 1/2 each; how much did they cost together?
Ramit bought 10 pens,8 pencils, and 4 books; pens were Rs.5 1/2 each, pencils were Rs.2 1/2 each and books were Rs. 11 1/2 each; how much did they cost together? - Usain
 Usain and Kyle rented a house together for 3 years. Usain paid more rent because he had a bigger room. They always split the rent at a ratio of 4:3. They paid £30247 in rent over this period. How much of this did Usain pay?
Usain and Kyle rented a house together for 3 years. Usain paid more rent because he had a bigger room. They always split the rent at a ratio of 4:3. They paid £30247 in rent over this period. How much of this did Usain pay? - Estimate and exact
 A) estimate 0.34 x 0.063 by rounding both numbers to one significant figure b) work out the exact value of 0.34 x 0.063 compare answers to parts a) and b)
A) estimate 0.34 x 0.063 by rounding both numbers to one significant figure b) work out the exact value of 0.34 x 0.063 compare answers to parts a) and b) - Sqrt of sum
 Find one-third of the square root of 81, the sum of 12, and the product of 3 and 12.
Find one-third of the square root of 81, the sum of 12, and the product of 3 and 12. - Linda
 Linda gave her sister 2/5 of her money, spent 1/3, and saved the remainder. If Linda saved $28.00, how much money did she have at first?
Linda gave her sister 2/5 of her money, spent 1/3, and saved the remainder. If Linda saved $28.00, how much money did she have at first? - Dostaneli
 If we get 5% of the amount that Petr has in his wallet and 4% of the amount that Paul has with him, we will have 46 CZK. However, if we get 4% from Peter's and 5% from Paul's, we will only have 44 CZK. How many crowns do Petr and Paul have with them?
If we get 5% of the amount that Petr has in his wallet and 4% of the amount that Paul has with him, we will have 46 CZK. However, if we get 4% from Peter's and 5% from Paul's, we will only have 44 CZK. How many crowns do Petr and Paul have with them? - Twice squared
 If the square of twice a number is 81, what is the number? Give a positive number x.
If the square of twice a number is 81, what is the number? Give a positive number x. - There 35
 There are three points on a straight line: A, BC. If CD = 8x, DE = 3, and CE = x + 10, what is CD? Simplify your answer and write it as a proper fraction, mixed number, or integer.
There are three points on a straight line: A, BC. If CD = 8x, DE = 3, and CE = x + 10, what is CD? Simplify your answer and write it as a proper fraction, mixed number, or integer. - Can you
 Can you help me solve this math problem? I need to know the answer after multiplying 2 2/3 by 2 1/4 and then adding 1 2/3 divided by 1 4/5. Thank you in advance for your assistance.
Can you help me solve this math problem? I need to know the answer after multiplying 2 2/3 by 2 1/4 and then adding 1 2/3 divided by 1 4/5. Thank you in advance for your assistance. - Comparing by height
 Ira is 1 2/5 m tall. Her mother is 4/5 m as tall as Ira. How many times is Ira's mother taller than her?
Ira is 1 2/5 m tall. Her mother is 4/5 m as tall as Ira. How many times is Ira's mother taller than her? - Bookshelf 3
 How many 1/35-inch thick books can fit on a 1 4/12-inch long bookshelf?
How many 1/35-inch thick books can fit on a 1 4/12-inch long bookshelf? - The painter
 Alex had 5/6 liter of white paint. He used 1/8 of it to paint the walls and 2/5 of the remaining to paint the fence. How much paint is left?
Alex had 5/6 liter of white paint. He used 1/8 of it to paint the walls and 2/5 of the remaining to paint the fence. How much paint is left? - Solution mg/ml
 If 70 ml of solution contains 280mg of drug, how many milligrams of drugs are in 50 ml of solution?
If 70 ml of solution contains 280mg of drug, how many milligrams of drugs are in 50 ml of solution? - Fresh chickens
 In the market, one stall is selling fresh chickens worth P120 per kilo. A person bought two fresh chickens weighing 1 1/2 and 1 1/4 kilos each. What is the total weight of the two chickens?
In the market, one stall is selling fresh chickens worth P120 per kilo. A person bought two fresh chickens weighing 1 1/2 and 1 1/4 kilos each. What is the total weight of the two chickens? - Library and gym
 In a town, 7/8 of the population has a library card, and 3/4 has a gym membership. What fraction of the population has either a library card or a gym membership?
In a town, 7/8 of the population has a library card, and 3/4 has a gym membership. What fraction of the population has either a library card or a gym membership? - Convert 8
 Convert 11/2 into a percent?
Convert 11/2 into a percent? - Eggs in basket
 If the eggs in a basket are removed twice at a time, one will remain. Two eggs will remain if the eggs are removed three at a time. If the eggs are removed four, five, or six at a time, the three, four, and five eggs will remain, respectively. However, no
If the eggs in a basket are removed twice at a time, one will remain. Two eggs will remain if the eggs are removed three at a time. If the eggs are removed four, five, or six at a time, the three, four, and five eggs will remain, respectively. However, no
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
