Maths practice for 14 year olds - page 7 of 369
Number of problems found: 7375
- The areas
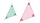 The areas of two similar triangles are 12 sq cm and 48 sq cm. If the height of the smaller one is 2.1 cm, then find the height of the bigger one.
The areas of two similar triangles are 12 sq cm and 48 sq cm. If the height of the smaller one is 2.1 cm, then find the height of the bigger one. - A shopkeeper 7
 A shopkeeper bought 80 cricket bats for 2.55 euros each. He sells 20 of them at a 5% gain. What must be the gain percentage of the remaining bats to get a 10% gain overall?
A shopkeeper bought 80 cricket bats for 2.55 euros each. He sells 20 of them at a 5% gain. What must be the gain percentage of the remaining bats to get a 10% gain overall? - An article
 An article is sold at 20% profit. If it were sold at a 25% profit, then he could get USD 35 more. Then, find the article's cost price.
An article is sold at 20% profit. If it were sold at a 25% profit, then he could get USD 35 more. Then, find the article's cost price. - Twice a number
 If 73 is one more than twice a number, what is 50% of the number?
If 73 is one more than twice a number, what is 50% of the number? - Twins 2
 The average age of a man and his two twin sons is 30 years. The ratio of the ages of father and one son is 5 : 2, what is the father's age?
The average age of a man and his two twin sons is 30 years. The ratio of the ages of father and one son is 5 : 2, what is the father's age? - At present
 At present, Ram is eight years younger than Susan, and Hari is two years younger. If the respective ratio between the present age of Ram and that of Hari is 3: 4, then what is Hari's present age?
At present, Ram is eight years younger than Susan, and Hari is two years younger. If the respective ratio between the present age of Ram and that of Hari is 3: 4, then what is Hari's present age? - Compound continuously
 Find the balance in the account after 10 years. P= $1900; r= 6% Compound continuously.
Find the balance in the account after 10 years. P= $1900; r= 6% Compound continuously. - Incircle to circumcircle
 Find the ratio of the areas of the incircle and the circumcircle of a square.
Find the ratio of the areas of the incircle and the circumcircle of a square. - Avg speed 2
 A car covers four successive 3 km stretches at 10 kmph, 20 kmph, 30 kmph, and 60 kmph, respectively. What is the average speed over this distance?
A car covers four successive 3 km stretches at 10 kmph, 20 kmph, 30 kmph, and 60 kmph, respectively. What is the average speed over this distance? - System of equations
 Solve the following system of equations: 2x-5y=4 5x-3y=4
Solve the following system of equations: 2x-5y=4 5x-3y=4 - Adam reaches
 If Adam walks at 3 km/h, he will reach school 15 minutes late. If he walks at 4 km/h (kmph), he will reach school 15 minutes earlier than usual. What is the distance between school and house?
If Adam walks at 3 km/h, he will reach school 15 minutes late. If he walks at 4 km/h (kmph), he will reach school 15 minutes earlier than usual. What is the distance between school and house? - Common difference
 What is the common difference of an AP (arithmetic progression) in which a₁₈ – a₁₄ = 32
What is the common difference of an AP (arithmetic progression) in which a₁₈ – a₁₄ = 32 - Two trains 13
 Two trains start at the same time toward each other from stations A and B at respective speeds of 36 km/h and 42 km/h. When they meet, it was found that one train has covered 48 km more than the other. Find the distance between the two stations.
Two trains start at the same time toward each other from stations A and B at respective speeds of 36 km/h and 42 km/h. When they meet, it was found that one train has covered 48 km more than the other. Find the distance between the two stations. - Equation of a line
 Find the equation of a line that passes through (1, 3) and is parallel to the line y = - 2x + 4.
Find the equation of a line that passes through (1, 3) and is parallel to the line y = - 2x + 4. - Milk with water 2
 If 50 liters of a mixture contains milk and water in a ratio of 3:2, how much milk must be added to the mixture to have milk and water in a ratio of 9:4?
If 50 liters of a mixture contains milk and water in a ratio of 3:2, how much milk must be added to the mixture to have milk and water in a ratio of 9:4? - Difference of squares
 If the difference between two numbers is 3 and the difference of their squares is 39, then find the larger number.
If the difference between two numbers is 3 and the difference of their squares is 39, then find the larger number. - Literacy ratio
 The town's population is 311250. The ratio of women to men is 43: 40. If 24% of men and 8% of women are literate, then find the total number of literate persons in the town.
The town's population is 311250. The ratio of women to men is 43: 40. If 24% of men and 8% of women are literate, then find the total number of literate persons in the town. - The vertices
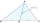 The vertices of a triangle are A (-1,3), B (1,-1), and C (5, 1). Find the length of the median through the vertex C.
The vertices of a triangle are A (-1,3), B (1,-1), and C (5, 1). Find the length of the median through the vertex C. - RT with rectangle
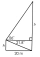 In the diagram, find the lengths h and b. One rectangle and one right triangle share one side. We know two angles and the length of the common side, as shown in the picture.
In the diagram, find the lengths h and b. One rectangle and one right triangle share one side. We know two angles and the length of the common side, as shown in the picture. - Fraction of a work
 Person A can do 1/2 of a piece of work in 8 days, while person B can do 1/3 of the same work in 8 days. In how many days can both do it together?
Person A can do 1/2 of a piece of work in 8 days, while person B can do 1/3 of the same work in 8 days. In how many days can both do it together?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
