Addition practice problems - page 19 of 78
Number of problems found: 1551
- Successful 83167
Eighth-grade test results: 8D =? 8B = 47 8A = 44 8E = 37 8C = 28 Class 8A achieved exactly the average result. How many points did the winning class 8D get? By what % is class 8B more successful than class 8C? - Motion on circle
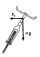The bend has a radius of r = 100 m and is inclined at an angle of 20° to the horizontal plane (= tilt angle). What is the safe (the "best") speed to go through this curve? Sketch the picture regarding NIVS, mark the forces, and calculate. - Jendo's 83123
Jenda, Milan, and Tomáš have a total of 203 Pokemon cards. Jenda has twice as many cards as Tomáš, and Milan has a quarter of Jendo's number of cards. a) How many cards does Jenda have? b) How many fewer cards do Milan have than Jenda and Tomáš? - Characters 82998
Adam wrote the following sum with five secret adders: a + bb + ccc + dddd + eeeee. He revealed that the characters "a, b, c, d, e" represent the different digits 1, 2, 3, 4, and 5 and that the resulting sum is divisible by 11. Which is the smallest and wh - Parametrically 82990
Calculate the sum of the x-coordinates of the intersections of the circle given by the equation (x - 1)²+ y² = 1 and the line given parametrically x = t, y = t , where t∈R. - Family in ratio
The ages of the father, mother, daughter, and son are in the ratio 11:9:3:2. The mom is 36 years old. What is the sum of their ages? - Determine 82975 Determine the sum of all positive odd numbers less than 78
- Calculate 82878
Calculate in degrees the size of the acute angle made by the hands of the clock at half past six. - Decimetres 82870
Next to the road are 15 pillars at a distance of 2.5 meters. The pillars are 15 cm wide and stand at the beginning and end of the path. Calculate the length of the path in decimetres. - Calculate 82845
Calculate the sum of the first 9 terms of the geometric sequence if a3 equals 2 and a4 equals 8. - Arrived 82746
The bus left Prague at 8:45 p.m. and arrived in Poprad at 5:35 a.m. How long did the bus take? - Consecutive 82712
The sum of five consecutive even numbers is -10. What are the numbers? - Expression 82698 Calculate the value of the expression V = 3x²- 2x + 3 for x = -2.
- Different 82683
There are candies from 1 to 10 in ten different packages. Each child took two packages. They got so many candies: Anka: 5 Zuzka: 7 Katka: 9 Monica: 15 How many candies does Lucka have? - Children 82574
Twenty-nine children attend the club. Eleven said that they have a dog, 14 children have a cat, and 12 children have a hamster. Two children have all three animals. Seven children do not have any animals at home. How many children have at least two of the - Collected 82554
Four friends were picking apples. Filip collected 3/16, Patrik 1/4, and Tomáš 1/3 of all apples. How many apples did Štefan collect? - Friends 82546 Two friends, Martin and Juraj, agreed that they would score +26 points for wins and -16 points for losses. Juraj lost nine times and won four times. What was his final score?
- Grandmother 82543
Michal is saving for a new computer. His parents gave him 130 euros, which was 26 percent of the total amount. He received 20 percent of the price of the computer from his grandmother, and his aunt added another 35 euros. How many euros does Michal still - Spacing 82540
There are 10 trees in a row with the same spacing x = =3 meters. How many meters does a person travel if he waters two trees at once - Fraction 82525
Of 32 students in the class, 3/4 of the children were on the trip. Write as a fraction what part of the students stayed at home. How many students were on the trip?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
