Examples of area of plane shapes
The area is the quantity that expresses the extent of a two-dimensional shape. The area can be understood as the amount of paint necessary to cover the surface with a single coat. The area of a shape can be measured by comparing the shape to squares of a fixed size 1 m2 or 1 cm2 etc. Every unit of length has a corresponding unit of area. We can measure areas in square meters (m2), square centimeters (cm2), square millimeters (mm2), square kilometers (km2), square feet (ft2), square yards (yd2), square miles (mi2), and so forth.The area of a shape is the “space enclosed within the perimeter or the boundary” of the given shape.
Number of problems found: 2505
- Blue region
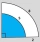Find the area of the blue region on the picture. - Circular garden 2
What is the area of the circular garden if the diameter of the circular garden is 4 meters? - The square - midpoints
The area of a square ABCD is 36 cm². Find the area of the square obtained by joining the midpoints of the sides of the square ABCD. - Chief Chief has a rectangular field. It is 13 m long and 21 m wide. Find the area of the rectangular field.
- Rectangle -S2
I need help calculating the area and perimeter of a rectangle with a length of 8 cm and a width of 5 cm. - Sq feet converions
What is the area in square feet of a room that is 10' 3" x 16' 9"? - The length 16
The length of a rectangle is 7.1 cm, and its breadth is 2.5 cm. What is the area of the rectangle?
- Parallelogram - simple
One of the sides and the corresponding height of a parallelogram are 4 cm and 3 cm respectively. Find the area of the parallelogram. - Square yards
What is 4 1/3 yards times 5 2/3 yards? - A rectangle 13 A rectangle measures 2 1/2 meters by 1 3/4 meters. What is its area?
- Area - simple
Find the area of the triangle. So, the base is 7 2/3 mi. The height is 7 mi. What is the Area? - A room
A room is 8 2/3 m by 5 1/4 m. What is the area of the room? - Share 5
Share 30 oranges between Shola and Ade in the ratio 2:3. Find Shola's share and Ade's share. - A rectangular 10 A rectangular flower garden is 4 1/2 ft by 4 3/4 ft. Find the perimeter and area of the garden.
- Concrete wall
A 10 1/2 by 16 concrete wall is to be built using concrete blocks. Find the area of the wall.
- Incircle to circumcircle Find the ratio of the areas of the incircle and the circumcircle of a square.
- Find area 2
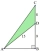Find the area of the green region in the given picture. Dimensions are shown. - A concert venue
The floor of a concert venue is 100 3/4 feet by 75 1/2 feet. What is the area of the floor? - Stacy
Stacy collected 4 bins of glass bottles to recycle. Tessa collected 1 1/5 times as many bins as Stacy. How many bins of bottles did Tessa collect? - A picture
A picture frame is 62 centimeters wide and 40 centimeters long. The frame is 4 centimeters thick on all sides. What is the area of the picture's display?
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
See also more information on Wikipedia.
