Rearrange variables - practice problems - page 2 of 145
Expressing from a formula means putting some variable on the left side. For example, the radius of a circle r = √ (S/π). For completeness, let us add that the symbol π is a constant, Ludolf's number = 3.14159.... A constant is like a variable, but always with the same value.Number of problems found: 2899
- Salaries - ratio3
The salaries of A, B, and C are in the ratio 2:3:5. If their salaries are increased by 15%, 10%, and 20% respectively, what will be the new ratio of their salaries? - Goods train
A goods train runs at a speed of 72 km/h and crosses a 250 m long platform in 26 seconds. What is the length of the goods train? - Angle of inclination
Find the angle of inclination of a ramp that rises 80 cm over a horizontal length of 200 cm. - Tower + pole
On horizontal ground, there is a vertical tower with a flagpole on its top. From a point 9 m from the foot of the tower, the angles of elevation of the top and bottom of the flagpole are 60° and 30° respectively. Find the height of the flagpole. - A rectangle 15
A rectangle is 5 cm longer than its width. Its area is 6 cm². What are the dimensions of the rectangle? - Rhombus = area, diagonal
The area of a rhombus is 144 cm². One diagonal is twice the length of the other. How long is the shorter diagonal? - The rhombus (a,d) Find the area of a rhombus, one side of which measures 20 cm and one diagonal of which is 24 cm.
- The length 20
The length and width of a rectangular park are in the ratio 8:5. A path 1.5 m wide, running all around the outside of the park, has an area of 594 m². Find the dimensions of the park. - A field
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m and whose non-parallel sides are 14 m and 13 m. Find the area of the field. - The average 17
The average monthly salary of 20 workers in an office is $4,590. If the manager's salary is added, the average salary becomes $4,920 per month. What is the manager's monthly salary? - Four numbers 3
What is the smallest number that must be added to each of the numbers 6, 15, 20, and 43 to make them proportional? - The angle 9
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving 20 m closer to the foot of the tower to a point B, the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower from point A - Surface = volume
If the volume and the surface area of a sphere are numerically equal, find its radius. - GP - terms
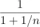Which term of the geometric progression 2, 8, 32, … is 131,072? - Triangle 90
A triangle has sides of 6 cm, 4.5 cm, and 7.5 cm. What are the sizes of its angles? - 765 chairs
765 chairs are to be arranged in rows such that the number of chairs in each row equals the number of rows. How many chairs need to be removed to complete this arrangement? - Susan 5
Susan has a water tank in her back garden that can hold up to 750 L of water. At the start of a rainy day (at 0:00) there are 165 L in the tank, and after a heavy day's rain (at 24:00) there are 201 L in the tank. Assuming that the rain fell at a constant - The boat
A boatman rows 2 km against the current in 40 minutes and returns to the same spot in 30 minutes. What is his rowing speed in still water? - A plane 3
A plane left 30 minutes later than the scheduled time. In order to reach the destination 1,500 km away on time, it had to increase its speed by 250 km/h from its usual speed. Find its usual speed. - Three inscribed objects
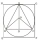A circle is inscribed in a square. An equilateral triangle with side 4√3 is inscribed in that circle. Find the length of the diagonal of the square.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
