Right triangle + expression of a variable from the formula - practice problems
Number of problems found: 642
- General right triangle
 In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse.
In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse. - A right triangle
 A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d?
A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d? - FGH right triangle
 Given a right triangle with leg lengths f and g, and hypotenuse h, if f = 7 cm and h = 11.2 cm, what is g?
Given a right triangle with leg lengths f and g, and hypotenuse h, if f = 7 cm and h = 11.2 cm, what is g? - The volume 8
 The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
- Perpendicular 5516
 In a right triangle, one perpendicular is 1 m shorter than the hypotenuse. The other perpendicular is 2 m shorter than the hypotenuse. Find the lengths of all sides of the triangle.
In a right triangle, one perpendicular is 1 m shorter than the hypotenuse. The other perpendicular is 2 m shorter than the hypotenuse. Find the lengths of all sides of the triangle. - Equilateral triangle
 Calculate the area of an equilateral triangle with a circumference of 72cm.
Calculate the area of an equilateral triangle with a circumference of 72cm. - Equilateral triangle
 The equilateral triangle has a 23 cm long side. Calculate its area.
The equilateral triangle has a 23 cm long side. Calculate its area. - The triangle
 The triangle has sides 5 cm long, 5 cm, and 8 cm long. What is the area of the triangle?
The triangle has sides 5 cm long, 5 cm, and 8 cm long. What is the area of the triangle? - Right isosceles triangle
 What can be the area of a right isosceles triangle with a side length of 8 cm?
What can be the area of a right isosceles triangle with a side length of 8 cm?
- The aspect ratio
 The aspect ratio of the rectangular triangle is 13:12:5. Calculate the internal angles of the triangle.
The aspect ratio of the rectangular triangle is 13:12:5. Calculate the internal angles of the triangle. - Integer sides
 A right triangle with an integer length of two sides has one leg √11 long. How much is its longest side?
A right triangle with an integer length of two sides has one leg √11 long. How much is its longest side? - Distance 8471
 The double ladder has a height of 3 m. What height will it reach when we spread it at a distance of 1 m?
The double ladder has a height of 3 m. What height will it reach when we spread it at a distance of 1 m? - Perpendicular 24671
 The right triangle has an area of 2304 cm2, and one perpendicular is 8 cm long. Express and calculate the second perpendicular.
The right triangle has an area of 2304 cm2, and one perpendicular is 8 cm long. Express and calculate the second perpendicular. - Calculate 4424
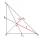 Calculate the area of the triangle ABC if a = 10 cm, c = 8 cm, ta = 6 cm.
Calculate the area of the triangle ABC if a = 10 cm, c = 8 cm, ta = 6 cm.
- Base and longest side
 The base of a right-angled triangle is 10 centimeters, and the longest side is 26 centimeters. What is the area of the triangle?
The base of a right-angled triangle is 10 centimeters, and the longest side is 26 centimeters. What is the area of the triangle? - Isosceles triangle
 Calculate the area and perimeter of an isosceles triangle ABC with base AB if a = 6 cm, c = 7 cm.
Calculate the area and perimeter of an isosceles triangle ABC with base AB if a = 6 cm, c = 7 cm. - Difference of legs
 In a right triangle, the hypotenuse length is 65 m, and the difference between legs is 23 m. Calculate the perimeter of this triangle.
In a right triangle, the hypotenuse length is 65 m, and the difference between legs is 23 m. Calculate the perimeter of this triangle. - Median in right triangle
 In the rectangular triangle, ABC has known the length of the legs a = 15cm and b = 36cm. Calculate the length of the median to side c (to hypotenuse).
In the rectangular triangle, ABC has known the length of the legs a = 15cm and b = 36cm. Calculate the length of the median to side c (to hypotenuse). - The pole
 A 4 m bullet supports the telegraph pole. It is at 3/4 of pole height, and the end is at a distance of 2.5 m from the pole post. Calculate the height of the telegraph pole.
A 4 m bullet supports the telegraph pole. It is at 3/4 of pole height, and the end is at a distance of 2.5 m from the pole post. Calculate the height of the telegraph pole.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
