Rearrange variables - practice problems
Work with mathematical expressions. Expressions are mathematical objects where some numbers are replaced by letters - variables. For example, the area of a circle is S = π r2, where r is a variable, the radius of the circle, and S is also a variable, the area. This is how we can describe the relationship between area and radius for all circles, generally. We can modify expressions, simplify, multiply, divide, add, etc. Also known as Formula Manipulation.Number of problems found: 2890
- Carnival
Kevin is going to a carnival that has games and rides. Each game costs $1.50 and each ride costs $3. Kevin spent $18 altogether at the carnival and the number of games he played is 4 times the number of rides he went on. Write a system of equations that c - Two terms and d
The 8th term of an AP is 17 and its 14th term is 29. Find the common difference of the AP. - Motorboat : current
The ratio of speeds of a motorboat to that of the current of water is 36:5. The motorboat goes along with the current in 5h 10min. Find the time to come back of the motorboat. - ABCD rhombus
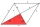ABCD is a rhombus with sides 10.5cm. If the length of the diagonal AC=15.8cm, using cosine formula. a. calculate the length of the diagonal BD correct to the nearest cm b. the angles of the rhombus to the nearest degree. - Insert two > GP
If 4, 36, 324 are in the geometric progression (GP) insert two more numbers in this progression so that it again forms a GP. - Common difference 4 The 28th term of an AP is -5. Find its common difference if its first term is 31.
- Angle of elevation 3
The angle of elevation of a pole from a point on the horizontal ground is 15°. After going up a distance of 10m towards the pole the angle of elevation became 30°.What is the height of the pole? - Four plates
Four equal maximum sized circular plates are cut off from a square paper sheet of area 784 sq cm. Calculate the circumference of each plates. - Square park
Amyra goes for a walk in a square park . The perimeter of the park is 1235 m. Find side of the park. - GP - negative term
The first term of a GP is -3 and the square of the second term is equal to its 4th term. Find the 7th term of the GP. - Three in a ratio
If A is 40% more than B, B is 20% less than C then, find the ratio A : C. - School - boys:girls
In a school 10% of boy is equal to the 1/4 of number of girls and 10% of the number of girls is equal to the 1/25 of boys. Find the ratio between the number of boys and girls. - The sum 53 The sum ofthree numbers of a GP series is 35 and their product is 1000. Find the numbers.
- The centroid
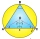The centroid of a triangle ABC is at the point (3,3,3). If the coordinates of A and B are (3, –5, 7) and (–1, 7, – 6) respectively, find the coordinates of the point C. - The surface 5
The surface area of a cylinder is 6140 cm², and the radius is 25 cm. What is the height? - A rope for cow
Find the length of a rope by which a cow must be tethered in order that it may be able to graze an area of 154 sq m . - The average 19 The average age of a class was 15 years. When 5 boys whose average age was 12 years 6 months were admitted in the class, the average was reduced by 6 months. How many students were there in the class originally?
- Cu ore
An ore contains 5% copper. How much ore is required to obtain 400 grams of copper? - The Earth and Moon
The diameter of the Moon is approximately 1/4 of the diameter of the Earth. What fraction of the volume of the Earth is the volume of the Moon? - Salaries - ratio3
The salaries A, B, C are in the ratio 2 : 3 : 5. If the increments of 15%, 10% and 20% are allowed respectively in their salaries, then what will be new ratio of their salaries?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
