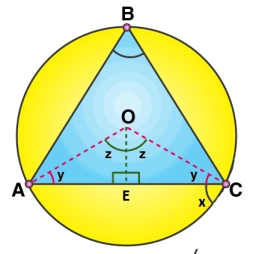
The centroid
The centroid of a triangle ABC is at the point (3,3,3). If the coordinates of A and B are (3, –5, 7) and (–1, 7, – 6) respectively, find the coordinates of the point C.
Correct answer:
Tips for related online calculators
Looking for help with calculating arithmetic mean?
Looking for a statistical calculator?
See also our trigonometric triangle calculator.
Looking for a statistical calculator?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- The coordinates 4
The coordinates of the vertices of ∆ABC are respectively (-4, -2), (6, 2) and (4, 6). Find the centroid G of ∆ABC. - Center
In the ABC triangle is point D[1,-2,6], which is the center of the |BC|, and point G[8,1,-3], which is the center of gravity of the triangle. Find the coordinates of the vertex A[x,y,z]. - Coordinates of a centroind
Let A = [3, 2, 0], B = [1, -2, 4], and C = [1, 1, 1] be 3 points in space. Calculate the coordinates of the centroid of △ABC (the intersection of the medians). - Two points
M and N are two points on the X-axis and Y-axis, respectively. Point P (3, 2) divides the line segment MN in a ratio of 2:3. Find: (i) the coordinates of M and N (ii) slope of the line MN.
- Triangle's centroid
In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t - MO Z7–I–6 2021
In triangle ABC, point D lies on the AC side and point E on the BC side. The sizes of the angles ABD, BAE, CAE, and CBD are 30°, 60°, 20°, and 30°, respectively. Find the size of the AED angle. - X-coordinate 81737
In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right.
