Geometric progression - practice problems
A geometric progression (or geometric sequence) is a sequence where each term after the first is found by multiplying the previous term by a fixed non-zero number called the common ratio. The general form is a, ar, ar², ar³, ... where a is the first term and r is the common ratio. The nth term is given by aₙ = a·r^(n-1). The sum of the first n terms is Sₙ = a(1-r^n)/(1-r) when r ≠ 1. Geometric progressions model exponential growth and decay, compound interest, and various scientific phenomena. When |r| < 1, an infinite geometric series can converge to a finite sum. Understanding geometric progressions is essential for sequences, series, and mathematical modeling.Number of problems found: 272
- Simple interest pa
If a sum of money at a rate of simple interest, doubles in 8 years, then it will become 3 times in how many years? - Insert two > GP
If 4, 36, 324 are in the geometric progression (GP) insert two more numbers in this progression so that it again forms a GP. - GP - negative term
The first term of a GP is -3 and the square of the second term is equal to its 4th term. Find the 7th term of the GP. - The sum 53
The sum ofthree numbers of a GP series is 35 and their product is 1000. Find the numbers. - A person 2
A person has 2 parents, 4 grandparents, 8 great grandparents, and so on. Find the number of his ancestors during the ten generations preceding his own. - A man 24
A man distributed 25300 EUR among his 3 sons A, B, C in such a way that the amounts of their parts at 10% simple interest in 2 years, 3 years, 4 years will be equal. A's share? - GP - terms
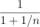Which term of the G.P., 2, 8, 32, ... up to n terms is 131072? - The value
The value of the property decreases every year at the rate of 5%. If its present value is 411540 USD, what was its value three years ago? - Doubling every day
If you start with 1 euro on day 1 and double your money daily, how many days before you get at least 1 million? - A town 3
A town with 12,000 people has been growing at a rate of 2.5% per year. How many years ago was the population 8,000? - Binary series The 4th term of a G.P. is 16 and the 7th term is 128 . Find the first term and common ratio of the series.
- Descent GP Determine the 18th term of the GP whose 5th term is 1 and common ratio is 2/3.
- Three Numbers GP The sum of three Numbers in geometric progression (GP) is 38, and their product is 1728. Find the Numbers.
- The sum 47 The sum of 3 numbers in an arithmetic progression (AP) is 15. If 1,4,19 are to be added to the above numbers respectively, it formed a geometric progression (GP). Find the numbers.
- Series - double GP In the following series, which number will replace the question mark? 4, 32, 16, 128, 64,?
- The 5th The 5th, 8th and 11th terms of a GP are a, b, c respectively. Show that a, b, c are in GP.
- An apple 2
An apple tree was planted two years ago. It increases at the rate of 20% every year .If at present, the height of the tree is 540 cm, what was it when the tree was planted? - A pattern If I have a pattern that starts with 1, 4, 9, 16, 25... and so on, which of the following numbers would not appear?
- A population
A population of fish starts at 8,000 and decreases by 6% per year. Use an exponential function to find the population of fish in 10 years. - Geometric progression For the following geometric progression, find the seventh (7th) term: 4, 12, 36, 108, .
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
