Length - math word problems - page 27 of 164
Number of problems found: 3262
- Selection 4
Selection triangle, which is similar to the given triangle RTG. ∆ RTG, r= 24 dm, t = 28 dm, g= 30 dm. ∆ SHV= 6 dm, h= 7.5 dm, v= 7 dm ∆ VSH= v= 7 dm, s= 6 dm, h= 7.5 dm ∆ HVS= h= 7.5 dm, v= 7 dm, s = 6 dm. ∆ VHS= v= 7 dm, h = 7.5 dm, s= 6 dm. ∆ HSV= h= 7. - Satellite runway speed
The satellite flies at a speed of 8 km/s. Will it fly down the runway in two seconds? - Triangle similarity selection
Choose a triangle that is similar to the given triangle. - ∆ TFC= t= 8 cm, f= 9 cm, c= 7 cm. : ∆ PKU= p= 45 cm, k= 35 cm, u= 40 cm. ∆ UPK= u= 40 cm, p= 45 cm, k= 35 cm. ∆ PUK= p= 45 cm, u= 40 cm, k= 35 cm. ∆ KPU= k= 35 cm, p= 45 cm, u= 40 cm. ∆ KUP= k= 35 - Julka twine cutting
Julka wanted to cut pieces 10 cm and 30 cm long from a 1 m long twine so that not a single piece would be too big for her. Did she succeed? - Triangle similarity decision Decide whether the triangles are similar. Choose between Yes/No. ∆ YUO: y= 9m, u= 17 m, o= 12 m, ∆ ZXV= z= 207 dm, x= 341 dm, v= 394 dm
- Archaeologists
Archaeologists need to find out the size of the vessel if the sherd found was in the shape of a circular section with a length of 12 cm and a height of 3 cm. What is the area of this section? - Base and legs
A right triangle has a base/legs/length of 12 cm, and the angle with the hypotenuse is 13 degrees. What is the length of the second hypotenuse? - Pyramid height volume
A regular four-sided pyramid has a volume of 2,160 liters and a base edge length of 12 dm. Calculate the height of the needle (sketch, calculation, answer). - Square ratio comparison
Two squares are given. The first has a side length of 5 cm, the second 10 cm. Write the ratio of: for a- of their sides for b- their perimeters for c- their areas - Gradient of the railway
Calculate the gradient of the railway line, which has an elevation of 22.5 meters in a section of 1.5 kilometers. For railways, the result is given in h (per mille). - Pyramid volume ratio
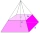A regular quadrilateral pyramid with base edge length a = 15cm and height v = 21cm is given. We draw two planes parallel to the base, dividing the height of the pyramid into three equal parts. Calculate the ratio of the volumes of the 3 bodies created. - Beetle cabbage pursuit
Tadeas the beetle set off from the house towards the cabbage leaf at a 20 m/min speed. Two minutes later, the Maximilian beetle followed him at 24 m/min speed. They both came to the cabbage leaf at the same time. How far was the letter from their house? - Pool stride area
Teo went around the pool twice. He took 160 steps in the process. He took 25 steps along the length. How much area does the pool take up, and how long is Tro's stride? 0.5m? - Rainwater cube buckets
The gardener collects rainwater in a cube-shaped container with an edge length of 80 cm. How many 16-liter buckets will he fill with water from a full reservoir? - City distance centimeters
The cities are 400 km apart; how many cm is it on a 1:400,000 scale map? - Bridge pillar length
One-fifth of the bridge pillar is embedded in the ground. One-third of its length is in the water, and 1.4 m protrudes above the surface. Determine the length of the bridge pillar. - Rod part division The rod was divided into three parts. The first part measured one-third of the length, the second one-third of the rest, and the third part was 20 cm. Calculate the rod's original length and the individual parts' lengths.
- Football field scale What is the scale of the city plan if the new football field with dimensions of 90m by 120m is shown on it as a rectangle with dimensions of 3cm by 4cm?
- Rectangle side percentage
One side of a rectangle is 45% of the length of its other side. What are the dimensions of a rectangle if its perimeter is 101.5 cm? - Forest square map
A forest with a square plan has an area of 4 square km. What side will the square have on a 1:50,000 scale map?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
