Rectangle practice problems - page 34 of 49

Number of problems found: 968

An equivalent
An equilateral triangle has the same perimeter as a rectangle whose sides are b and h (b > h). Considering that the area of the triangle is three times the area of the rectangle. What is the value of b/h?
Calculation 31381
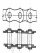A chain was stretched between two identical gears with a diameter of 40 cm. The distance between the wheel centers is 1.8 m. Calculate the length of the chain. Procedure and calculation
Rectangle - desc circle
The length of the sides of the rectangle is at a ratio of 1:3. The circle's radius circumscribed to the rectangle is 10 cm. Calculate the rectangle's perimeter.
The conical roof
The conical roof above the warehouse has a diameter of the lower part (base) d = 11.2 m and a height v = 3.3 m. How many rectangular steel plates with dimensions of 1.4 m and 0.9 m were needed to produce this roof if the seams and waste required an increa
Dimensions 16813
Calculate how many bricks we will need to build a room that should be 1.8 m wide, 2 m long, and 2.4 m high. The dimensions of the brick are 25 cm x 60 cm.
Rectangles 3579
I need to fill a circle with a diameter of 4900 cm with how many rectangles, 125x60 or 100x50 cm.
Rectangle 3148
The garden tank is filled to the brim with water. The bottom of the tank is a rectangle with sides of 150 cm and 160 cm, and the height of the tank is 0.8 m. How many 15 l cans can we use to empty the garden tank?
Cuboid - volume and areas
The cuboid has a volume of 250 cm³, a surface of 250 cm², and one side 5 cm long. How do I calculate the remaining sides?
Two-thirds 3388
The kneaded cake dough has a volume of 1.8 l. When baking, it increases its volume by about two-thirds. Can a baked wheel fit on a baking sheet measuring 36x30x8cm? How tall will the cake be after baking?
Allan
Allan keeps tropical fish. His aquarium is 4 feet long, 1 foot wide, and 2 feet tall. Each fish needs at least 0.5ft³ of water. What is the maximum number of fish he can keep in the aquarium? Please show your solution. Please
A box 4
A box open at the top has a rectangular base of 200 mm x 300 mm and an altitude of 150 mm. If the base and the sides are 10 mm thick, find the box's total surface area.
Wooden box
The block-shaped box was placed on the ground, leaving a rectangular print with 3 m and 2 m. When flipped over to another wall, a print with dimensions of 0.5 m and 3 m remained in the sand. What is the volume of the wooden box?
Iceberg
What is the surface area of a 50 cm iceberg (in the shape of a cuboid) that can carry a man with luggage with a total weight of 120 kg?
Bricks wall
There are 5000 bricks. How high wall thicknesses of 20 cm around the area, which has dimensions of 20 m and 15 m, can use these bricks to build? Brick dimensions are 30 cm, 20 cm, and 10 cm.
Cardboard - boxes
The closed cardboard box has the shape of a block measuring 25 cm, 1.2 dm, and 0.5 m. How much cardboard is needed to make 20 such boxes? You need to add 5% to bends.
Rectangle 4523
How high must the box, the bottom of which is a rectangle with sides of 40 cm, 625 mm, have a volume of 1 hl?
Two bodies
The rectangle with dimensions 8 cm and 4 cm is rotated 360º first around the longer side to form the first body. Then, we similarly rotate the rectangle around the shorter side b to form a second body. Find the ratio of surfaces of the first and second bo
Cuboid - edges
The cuboid has dimensions in a ratio of 4:3:5. The shortest edge is 12 cm long. Find: The lengths of the remaining edges The surface of the cuboid The volume of the cuboid
Cuboid walls
The block's base is a rectangle whose sides have lengths in the ratio of 13:7. Find the volume of the block in liters if the longer side of the base measures 65 cm and the height of the block is 1.2 m
A screen
A screen is 1680 x 1050 pixels. What are the coordinates (and size in pixels) of a central area which is exactly 33% of the screen size?

«
1
2
...
33
34
35
...
48
49
»

Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.