Sets - practice problems
Set theory is the mathematical study of collections of objects, called elements or members, treated as a single entity. Sets can be defined by listing elements {1, 2, 3} or by a property {x | x is even}. Fundamental operations include union (combining sets), intersection (common elements), difference (elements in one but not another), and complement. Sets can be finite or infinite, and relationships include subset, proper subset, and equality. Venn diagrams provide visual representations of set relationships and operations. Set theory forms the foundation of modern mathematics and is essential for probability, logic, and database theory.Number of problems found: 307
- Reading newspaper
40% of the people read newspaper x and 50% read newspaper y, and 10% read both the papers. What percentage of people read neither of the newspapers? - Hiking trails
There are 12 thousands kilometers of hiking trails in a national park. Each trail is rated for difficulty: 3/8 of the trails are rated easy, 1/6 are rated moderate, 1/4 are rated hard, and 5/24 are rated difficult. What fraction of the trails are rated ea - Blue region
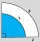Find the area of the blue region on the picture. - Failed in examination
In an examination, 20% of total students failed in history,15% failed in English and 5% of total number of students failed in both subjects. Find the percentage of total number of students who passed in both the subjects. - A merit scholarship
Last year’s freshman class at Big State University totaled 5,307 students. Of those, 1,264 received a merit scholarship to help offset tuition costs during their freshman year (although the amount varied per student). The amount a student received was N($ - Two games In a class of 65 students, 30 students play cricket, 20 students play tennis, and 10 students play both games. Then, find the number of students who play neither.
- Test and exam
1100 boys and 700 girls appeared in a test. If 42% of boys and 36% of girls passed, then find the percentage of students who failed. - Two points
M and N are two points on the X-axis and Y-axis, respectively. Point P (3, 2) divides the line segment MN in a ratio of 2:3. Find: (i) the coordinates of M and N (ii) slope of the line MN. - Football and cricket In a school 40% of the students play football and 50% play cricket. If 18% of the students neither play football nor cricket, then find the percentage of the students playing both.
- LS and y-axis intersection In what ratio is the line segment joining P (5, 3) and Q (–5, 3) divided by the y-axis? Also, find the coordinates of the intersection point.
- The well 3 When the health department tested private wells in a county for two impurities commonly found in drinking water, it found that 20% of the wells had neither impurity, 40% had impurity A, and 50% had impurity B. (Obviously, some had both impurities. ) If a
- Two sets 2 If X and Y are two sets such that X ∪ Y has 50 elements, X has 28 elements and Y has 32 elements, how many elements does X ⋂ Y have?
- An examination
In an examination 65% students passed in English and 56% in mathematics. And 25% failed in both the subjects. If 414 passed in both the subjects, then find the total number of students. - Richard
Richard is conducting an experiment. Every time he flips a fair two-sided coin, he also rolls a six-sided die. What is the probability that the coin will land on tails and the die will land on an even number? - The row
The row of shrubs will be 20 feet long. Maya planted three sets of shrubs. One shrub needs to be 7 1/2 feet from the other shrub. How can you use fractions to show how far apart each shrub is from each other? - X intercept Given: 3y+2x=-6 Calculate the X-intercept.
- Library and gym In a town, 7/8 of the population has a library card, and 3/4 has a gym membership. What fraction of the population has either a library card or a gym membership?
- And or logic
If A and B are events with P(A)=0.3, P(A OR B)=0.76, and P(A AND B)=0.04, find P(B). Enter your answer in decimal form, rounded to one place. - Three 241
Three-fifths of the t-shirts in a t-shirt shop are blue. Five-eights of those T-shirts are on sale. One-third of the blue of the blue shirts that are on sale are size medium. What fraction of the shop's blue T-shirts are on sale and size medium? - And - or probability rules Given P(A)=0.4, P(B)=0.56, and P(A and B)=0.274, find the value of P(A or B), rounding, if necessary.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
