Normal distribution calculator
Enter the mean μ (average), standard deviation σ, and cutoff points, and this normal distribution calculator will compute the area (probability) under the normal distribution curve.Normal distribution practice problems:
- An insurance
 An insurance company receives, on average, two claims per week from a particular factory. Assuming that a Poisson distribution can model the number of claims, find the probability it receives. three claims in a given week, more than four claims in a given
An insurance company receives, on average, two claims per week from a particular factory. Assuming that a Poisson distribution can model the number of claims, find the probability it receives. three claims in a given week, more than four claims in a given - Decides
 Decide by calculation how many candidates out of a total of 1000 candidates for the position of CEO meet the eligibility requirements for the desired performance of this top management position with at least 67% probability - provided, of course, that the
Decide by calculation how many candidates out of a total of 1000 candidates for the position of CEO meet the eligibility requirements for the desired performance of this top management position with at least 67% probability - provided, of course, that the - 10km race
 Joan's finishing time for the Bolder Boulder 10 km race was 1.77 standard deviations faster than the women in her age group. 415 women ran in her age group. Assuming a normal distribution, how many women ran more quickly than Joan?
Joan's finishing time for the Bolder Boulder 10 km race was 1.77 standard deviations faster than the women in her age group. 415 women ran in her age group. Assuming a normal distribution, how many women ran more quickly than Joan? - Entrance exam
 In a college entrance exam, the participants are rated as excellent, very good, good, and fair. Consider that the scores in the exam are normally distributed with a mean of 78 and a standard deviation of 7.5. The participants receiving the top 5% of the s
In a college entrance exam, the participants are rated as excellent, very good, good, and fair. Consider that the scores in the exam are normally distributed with a mean of 78 and a standard deviation of 7.5. The participants receiving the top 5% of the s - 3 sigma
 Students' performance scores in a statistic test have a mean of 70 and a standard deviation of 4.0. The scores obtained can be modeled by a normal distribution. Find the probability that the score of a randomly selected student is i. more than 80 marks ii
Students' performance scores in a statistic test have a mean of 70 and a standard deviation of 4.0. The scores obtained can be modeled by a normal distribution. Find the probability that the score of a randomly selected student is i. more than 80 marks ii - Z score transformation
 Suppose a distribution has a mean µ = 8 and standard deviation σ = 4. What is the value of x if it is z = +1.50?
Suppose a distribution has a mean µ = 8 and standard deviation σ = 4. What is the value of x if it is z = +1.50? - Lengths 6
 Lengths of 130 tubes are measured. The arithmetic mean is 17.27 cm, and the standard deviation is 1.2 cm. How many tubes do have a length: a) between 16.5 cm and 18.1 cm b) greater than 17 cm
Lengths of 130 tubes are measured. The arithmetic mean is 17.27 cm, and the standard deviation is 1.2 cm. How many tubes do have a length: a) between 16.5 cm and 18.1 cm b) greater than 17 cm - Fish service
 According to a report by the U. S. Fish and Wildlife Service, the mean length of six-year-old rainbow trout in the Arolik River in Alaska = 484.6 millimeters with a standard deviation = 31.2 millimeters. Assume these lengths are normally distributed. What
According to a report by the U. S. Fish and Wildlife Service, the mean length of six-year-old rainbow trout in the Arolik River in Alaska = 484.6 millimeters with a standard deviation = 31.2 millimeters. Assume these lengths are normally distributed. What - Life expectancy
 The life expectancy of batteries has a normal distribution with a mean of 350 minutes and a standard deviation of 10 minutes. What is the range in minutes 68% of the batteries will last? What is the range in minutes? How long will approximately 99.7% of b
The life expectancy of batteries has a normal distribution with a mean of 350 minutes and a standard deviation of 10 minutes. What is the range in minutes 68% of the batteries will last? What is the range in minutes? How long will approximately 99.7% of b - Mean
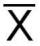 The mean of 50 items for a student's food is 38.6. When checking the work, he found that he had taken one item as 50 to read as 40 correctly in these circumstances. What should the correct arithmetic mean?
The mean of 50 items for a student's food is 38.6. When checking the work, he found that he had taken one item as 50 to read as 40 correctly in these circumstances. What should the correct arithmetic mean? - Lightbulbs
 The physical plant at the main campus of a large state university recieves daily requests to replace fluorescent lightbulbs. The distribution of the number of daily requests is bell-shaped and has a mean of 48 and a standard deviation of 10. Using the emp
The physical plant at the main campus of a large state university recieves daily requests to replace fluorescent lightbulbs. The distribution of the number of daily requests is bell-shaped and has a mean of 48 and a standard deviation of 10. Using the emp
more math problems »
