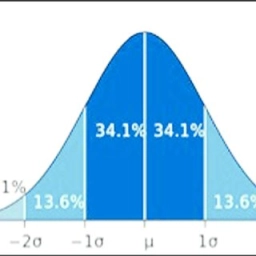
3 sigma

Students' performance scores in a statistic test have a mean of 70 and a standard deviation of 4.0. The scores obtained can be modeled by a normal distribution. Find the probability that the score of a randomly selected student is

i. more than 80 marks
ii. less than 65 marks

Find also the number of students who scored above 80 marks if a total of 1200 students sat for the test.

Correct answer:

a =  0.0062
b =  0.1056
c =  7

Step-by-step explanation:

$$\begin{gathered} \mu =70 \\ \sigma =4.0 \\ {z}_1=\frac{80-\mu }{\sigma }=\frac{80-70}{4}=\frac{5}{2}=2\frac{1}{2}=2.5 \\ 80=\mu +2.5\cdot \sigma \\ a=0.0062 \end{gathered}$$

Use the normal distribution table.

$$\begin{gathered} z_2=\frac{65-\mu }{\sigma }=\frac{65-70}{4}=-\frac{5}{4}=-1\frac{1}{4}=-1.25 \\ 65=\mu -1.25\cdot \sigma \\ b=0.1056 \end{gathered}$$

Use the normal distribution table.

$$\begin{gathered} n=1200 \\ c=[a\cdot n]=[0.0062\cdot 1200]=7 \end{gathered}$$

Try another example