Pravděpodobnost skóre testu
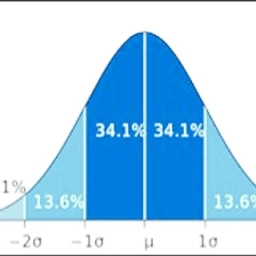
Výkonové skóre studentů ve statistickém testu má průměr 70 a standardní odchylku 4,0. Získané skóre lze modelovat pomocí normálního rozdělení. Najděte pravděpodobnost, že skóre náhodně vybraného studenta je
i. více než 80 bodů
ii. méně než 65 bodů
Zjistěte také počet studentů, kteří dosáhli více než 80 bodů, pokud se testu zúčastnilo celkem 1200 studentů.
Vaše odpověď:
i. více než 80 bodů
ii. méně než 65 bodů
Zjistěte také počet studentů, kteří dosáhli více než 80 bodů, pokud se testu zúčastnilo celkem 1200 studentů.
Vaše odpověď:
Tipy na související online kalkulačky
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
statistikakombinatorikaaritmetikaÚroveň náročnosti úkolu
Související a podobné příklady:
- Normální rozdělení
Předpokládejme, že skóre v testu má normální rozdělení se střední hodnotou X=74 a standardní odchylkou s=18. Jaké procento studentů má skóre vyšší než 90? Jaké procento studentů má skóre mezi 70 a 85? Dvacet procent studentů dělá lepší, než dosáhli na zko - Předpokládejme - test
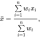Předpokládejme, že ve fyzikálním testu, kterého se zúčastnilo 30 studentů, by čtyři dosáhly 75 %, osmi 60 %, dvanácti 50 % a šesti 30 %. Vypočítejte průměr skupiny a standardní odchylku. - Průměr známek GPA
Průměrná GPA (Grade Point Average = průměr známek) je 2,78 se standardní odchylkou 0,45. Pokud je GPA normálně distribuována, jaké procento studentů má následující GPA? Vyřešte pomocí Z-skóre a nahlaste příslušné procento: a. Méně než 2,30 b. Méně než 2,0 - Životnost cvrčka
Průměrná délka života kriketu je 90 dní se standardní odchylkou 13 dní. Pokud předpokládáme, že životnost kriketu je normálně rozdělena, a. Jaká je pravděpodobnost, že náhodně vybraný cvrček bude mít životnost méně než 75 dní? b. Jaká je pravděpodobnost, - Binomické rozdělení studentů
Na kalifornské komunitní vysoké škole přestoupí 60 % studentů na vysokou školu v systému CSU. Počet studentů ve vzorku, kteří budou prostupovat, se řídí binomickým rozdělením. Pokud je náhodně vybráno 8 studentů, najděte rozptyl populace σ² náhodné proměn - Z-skóre transformace
Předpokládejme, že rozdělení má průměr µ = 8 a standardní odchylku σ = 4. Jaká je hodnota x, pokud z = +1,50? - Poissonovo rozdělení
Pojišťovna dostane v průměru dvě škody týdně z konkrétní továrny za předpokladu, že počet škod lze modelovat podle Poissonova rozdělení, najděte pravděpodobnost, že dostane tři nároky v daném týdnu, více než čtyři nároky v daném týdnu, čtyři nároky za dan
