Maths practice for 14 year olds - page 24 of 370
Number of problems found: 7400
- Pet store 2
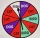 A pet store is having a prize giveaway. The spinner shows the type of toy a customer can win for their pet. Spinner is divided to 10 sections, and there are 5 cat sections. If a customer spins the spinner and it lands on a cat, they will win a free cat to
A pet store is having a prize giveaway. The spinner shows the type of toy a customer can win for their pet. Spinner is divided to 10 sections, and there are 5 cat sections. If a customer spins the spinner and it lands on a cat, they will win a free cat to - Write 7
 Write an expression representing the distance between −7 and 3 on a number line.
Write an expression representing the distance between −7 and 3 on a number line. - The temperature 46
 The temperature in Mumbai at 5 AM is 25 degrees Celsius. It rises 3 degrees Celsius every hour for the next two hours and then 5 degrees Celsius per hour for the next 3 hours. What is the temperature after 5 hours?
The temperature in Mumbai at 5 AM is 25 degrees Celsius. It rises 3 degrees Celsius every hour for the next two hours and then 5 degrees Celsius per hour for the next 3 hours. What is the temperature after 5 hours? - Percentage decrement
 Decrease 360 by 10%
Decrease 360 by 10% - One side 3
 One side of a triangular banner is 1 1/2 times longer than the second side and 2cm shorter than the third side. The perimeter of the triangle is 98cm. How long is the shortest side?
One side of a triangular banner is 1 1/2 times longer than the second side and 2cm shorter than the third side. The perimeter of the triangle is 98cm. How long is the shortest side? - Circle graph
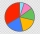 Erica surveyed students at her school about their favorite type of music. She made a circle graph to show the results. The central angle for the section of the graph that represents country music measures 72°. If 45 classmates chose the country as their f
Erica surveyed students at her school about their favorite type of music. She made a circle graph to show the results. The central angle for the section of the graph that represents country music measures 72°. If 45 classmates chose the country as their f - Markdown
 February is sale month at the clothing store. All items are marked down 20 percent. If the sale price for a purse is $42, what was the price before the markdown?
February is sale month at the clothing store. All items are marked down 20 percent. If the sale price for a purse is $42, what was the price before the markdown? - Water 70
 Water is poured into a hemisphere-shaped bowl at a rate of 5m³ per second. If the bowl has a depth of 8m, how long does it take to fill up the bowl to the rim?
Water is poured into a hemisphere-shaped bowl at a rate of 5m³ per second. If the bowl has a depth of 8m, how long does it take to fill up the bowl to the rim? - A right triangle
 A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d?
A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d? - Forty 8
 Forty students took the math test. Thirty-two students received an A, and the rest received a B. What percent of the students received a B?
Forty students took the math test. Thirty-two students received an A, and the rest received a B. What percent of the students received a B? - School trip
 Out of 270 students in 6th grade, only 60% are going on the field trip. How many students are NOT going on the field trip?
Out of 270 students in 6th grade, only 60% are going on the field trip. How many students are NOT going on the field trip? - Angles - triangle
 Find the measure of the angles of the triangle ABC if: the measure of angle A is the measure of angle C and the measure of angle B =½ of the measure of angle C.
Find the measure of the angles of the triangle ABC if: the measure of angle A is the measure of angle C and the measure of angle B =½ of the measure of angle C. - Sam thinks
 Sam thinks the club needs more female members. The club has 66 members. The ratio of male to female club members is 5:1. How many members are female?
Sam thinks the club needs more female members. The club has 66 members. The ratio of male to female club members is 5:1. How many members are female? - A chemist 2
 A chemist has two alloys of bronze, one that is 12% tin and 88% copper and a second that is 10% tin and 90% copper. If these two alloys are melted and thoroughly mixed together, between what two values are the percent of tin in the mixture?
A chemist has two alloys of bronze, one that is 12% tin and 88% copper and a second that is 10% tin and 90% copper. If these two alloys are melted and thoroughly mixed together, between what two values are the percent of tin in the mixture? - Xero had
 Xero had a piece of ribbon. He used 0.4 of it to tie 2 small boxes and 2 large boxes. The length of ribbon needed for a large box is 3 times the length of ribbon needed for a small box. Xero used 5/6 of the remaining ribbon to decorate the presents. a) Wh
Xero had a piece of ribbon. He used 0.4 of it to tie 2 small boxes and 2 large boxes. The length of ribbon needed for a large box is 3 times the length of ribbon needed for a small box. Xero used 5/6 of the remaining ribbon to decorate the presents. a) Wh - Pets stores
 Pets Plus and Pet Planet are having a sale on the same aquarium. At Pets Plus, the aquarium is on sale for 30% off the original price, and at Pet Planet, it is discounted by 25%. If the sales tax rate is 8%, which store has the lower sale price? How much
Pets Plus and Pet Planet are having a sale on the same aquarium. At Pets Plus, the aquarium is on sale for 30% off the original price, and at Pet Planet, it is discounted by 25%. If the sales tax rate is 8%, which store has the lower sale price? How much - Pupils
 There are 40 pupils in a class. 30% of them are boys. How many pupils in the class are girls?
There are 40 pupils in a class. 30% of them are boys. How many pupils in the class are girls? - In which
 In which of the following expressions does the number 16 fill in the blank so that the equation is true? Select all that apply. A) 8(___ + 3) = 32 + 24 B) 8(2 + 9) = ___ + 72 C) 4(7 + 4) = 28 + ___ D) 8(5 + 6) = 40 + ___
In which of the following expressions does the number 16 fill in the blank so that the equation is true? Select all that apply. A) 8(___ + 3) = 32 + 24 B) 8(2 + 9) = ___ + 72 C) 4(7 + 4) = 28 + ___ D) 8(5 + 6) = 40 + ___ - Represent 14
 Represent 10% as a fraction reduced to the lowest term.
Represent 10% as a fraction reduced to the lowest term. - A radio antenna
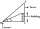 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
