Maths practice for 14 year olds - page 44 of 376
Number of problems found: 7519
- Salt solution
The 50% salt solution must be diluted with distilled water to make 20 liters of 35% solution. How many liters of original solution and how many liters of water do we need? - Jane bought
Jane bought several identical lined notebooks, several identical squared notebooks, and several identical compasses at a stationery store. Two lined notebooks and two squared notebooks cost a total of 180 crowns. Two squared notebooks cost the same as thr - The ladder and wall
A 6.5-meter-long ladder rests against a vertical wall. Its lower end rests on the ground 1.6 meters from the wall. Determine how high the top of the ladder reaches and at what angle it rests against the wall. - Determine 83081
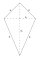A paper kite is shaped like a deltoid ABCD, with two shorter sides 30 cm long, two longer sides 51 cm long, and a shorter diagonal 48 cm long. Determine the sizes of the internal angles of the given deltoid. - Difference 83079
On the traffic sign that informs about the road's gradient, the figure is 6.7%. Determine the slope angle of the path. What height difference is covered by the car that traveled 2.8 km on this road? - Penetrates 83078
A hammer with a mass of 600 g hits the head of a nail at a speed of 5 m/s. If the nail penetrates 3 cm into the wall, what is the average resistive force of the masonry? - Overcoming 83076
A battering ram weighing 400 g falls from a height of 3 m. Upon impact, the stake hits a depth of 60 cm. What is the average force overcoming the soil resistance?
- Participating 83071
One hundred seventy-five school pupils signed up for the school trip. The ratio of boys to girls was 9: 16. In the end, 19 registered students did not come on the trip, so the ratio of the number of participating boys and girls was 9: 17. How many boys an - Calculate 83044
The cube comprises 64 small cubes, each with an edge length of 15 mm. Calculate the wall length and body diagonals. - Simultaneously 83038
The cable car can take a given group of skiers out in 20 minutes and the lift in 30 minutes. How long will the lift and cable car take this group out simultaneously? - Concerning 83022
A man with a mass of 80 kg crosses at a speed of 5 m/s through the car of a train traveling at 15 m/s. Indeed, the kinetic energy of a man: and, concerning the car b, relative to the surface of the earth, if the man is traveling in the direction of travel - Interpretation 83015
A cargo boat with a total weight of 4,500t sailed from the river to the sea. Calculate by how many tons it is possible to increase the weight of the cargo on the boat at sea so that the draft remains the same as in the river. The density of river water is - Equilateral 83013
Traffic signs are equilateral triangles with a side length of 900 mm. How many euros does a galvanized sheet cost to produce 50 pieces of such brands if we consider adding 15% of the material for waste? The price of 1 square meter of sheet metal is 6.5 eu - Ostrava 83008
A truck with a speed of 45 km/h left Ostrava. When he had passed 15 km, a car with a 90 km/h speed came behind him. How long does a car catch up with a truck take? How far from Ostrava? - Encyclopedias 83005
The seller sells books for 20 euros and encyclopedias for 50 euros. How many books and encyclopedias did he sell if he sold 121 books? He won €8,000 for both types.
- Population 83002
Calculate how many people were born in the state; if the total population was 10,000,000 this year, the natural increase was 2%, and 5,000 people died. - Centimeters - trapezoid
The area of the trapezoid is 132 cm². The difference in the length of both bases is 6 cm, and the height is 2 cm longer than the shorter base. Find the height of the trapezoid in centimeters. - Already 82989
The book has 1200 pages, of which Róza has already read 60%. How many pages has Rose not read so far? - Daughter 82977
The ages of the father, mother, daughter, and son are in the ratio 11:9:3:2. The mom is 36 years old. What is the sum of their ages? - Determine 82975
Determine the sum of all positive odd numbers less than 78
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
